A Gravitational Optimization Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
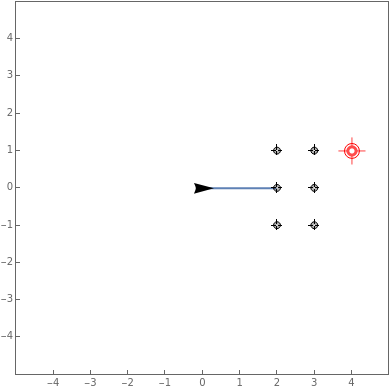
Consider a collection of fixed particles of mass 1 at prescribed positions (shown as black locators). Another particle of mass 1 starts at  with velocity 1 in a direction θ (counterclockwise from the
with velocity 1 in a direction θ (counterclockwise from the  axis). It then travels according to Newton's laws, subject to an inverse-square force of magnitude
axis). It then travels according to Newton's laws, subject to an inverse-square force of magnitude  from each of the fixed masses. What is the shortest time in which the moving particle can be made to reach a prescribed target (the red locator)? This Demonstration lets you vary the initial direction to thereby find an approximate value of the optimal angle and minimum time by trial and error.
from each of the fixed masses. What is the shortest time in which the moving particle can be made to reach a prescribed target (the red locator)? This Demonstration lets you vary the initial direction to thereby find an approximate value of the optimal angle and minimum time by trial and error.
Contributed by: Antonín Slavík and Stan Wagon (April 2014)
(Charles University, Prague and Macalester College, St. Paul, Minnesota)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The trajectory is calculated numerically and the motion stops as soon as the moving particle hits the target or one of the fixed masses, or if the prescribed time limit is exceeded. You can change the positions of the fixed particles as well as the target by dragging the mouse or by choosing one of the predefined configurations. It is also possible to add fixed particles by ⌘-clicking or Alt-clicking, or to remove them by holding the shift key.
The default grid configuration has fixed masses at positions  ,
,  ,
, 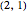 ,
,  ,
,  ,
,  , and the target at position
, and the target at position  ; this problem appeared in Appendix D of [1]. The optimal solution (shown in the first snapshot) is approximately
; this problem appeared in Appendix D of [1]. The optimal solution (shown in the first snapshot) is approximately  with the final time
with the final time  ; this fact can be verified by a numerical minimization procedure.
; this fact can be verified by a numerical minimization procedure.
Reference
[1] F. Bornemann, D. Laurie, S. Wagon, and J. Waldvogel, The SIAM 100-Digit Challenge: A Study in High-Accuracy Numerical Computing, Philadelphia: Society for Industrial and Applied Mathematics, 2004.
Permanent Citation