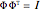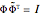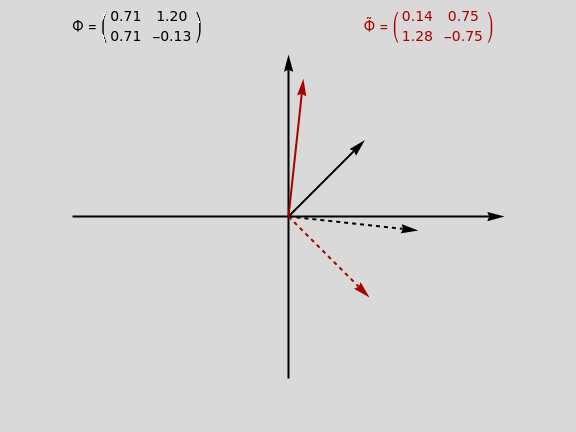
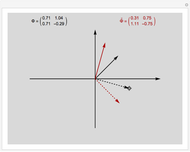
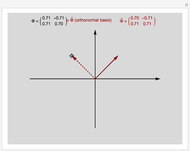
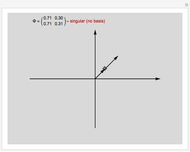
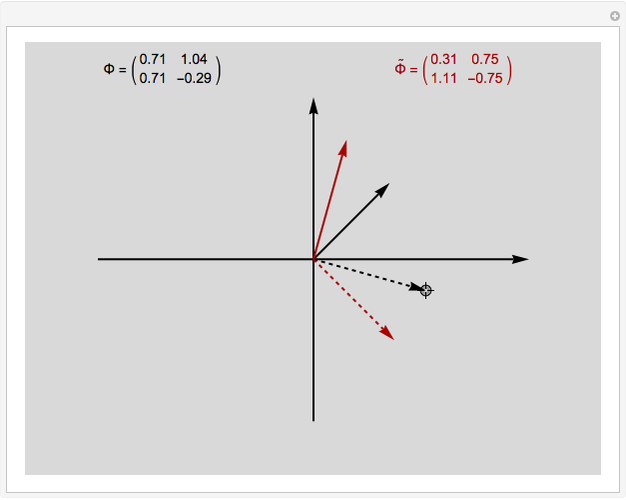
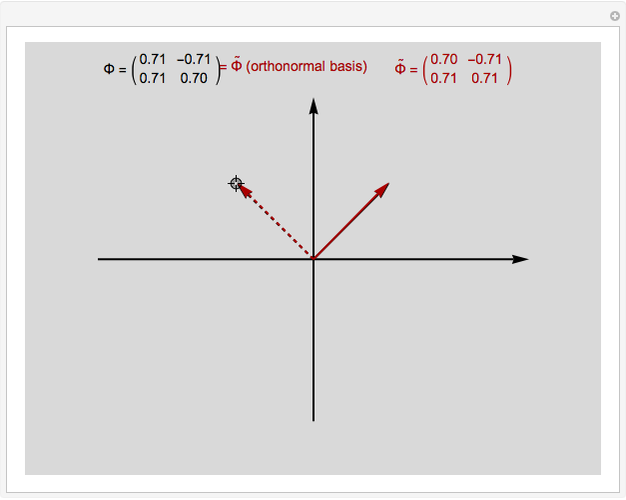
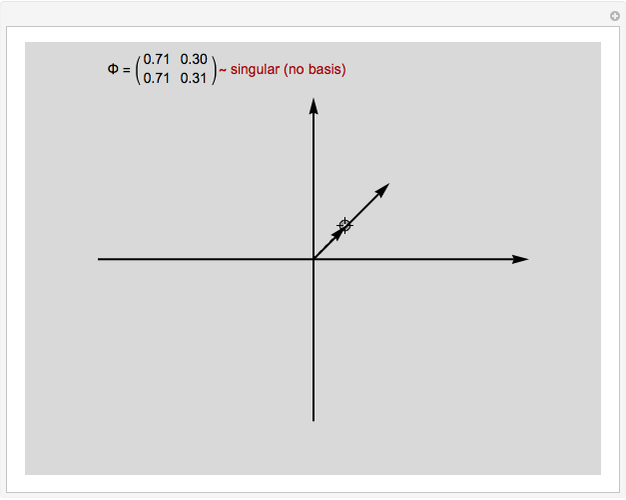
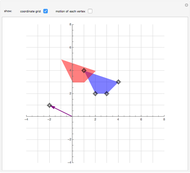
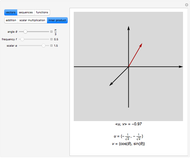
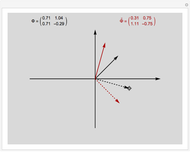
In mathematics, a pair of biorthogonal bases (a basis and its dual basis) can provide a representation for vectors in the plane; this is an alternative to what can be done with a single orthonormal basis. While in an orthonormal basis the basis vectors are mutually orthogonal, in a pair of biorthogonal bases the first vector in the basis (solid black in figure) is orthogonal to the second vector in the dual basis (dashed red in figure). Similarly, the second vector in the basis (dashed black in figure) is orthogonal to the first vector in the dual basis (solid red in figure). Furthermore, the corresponding vectors in the two bases have an inner product equal to 1. As each basis can be represented by a matrix whose columns are the basis vectors, the two bases are given when they exist (which is when the matrices are invertible).