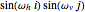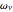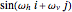Separable and Nonseparable 2D Sequences
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
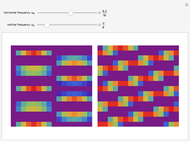
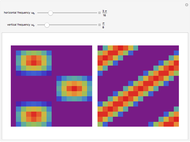
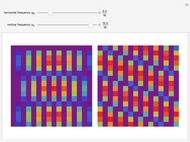
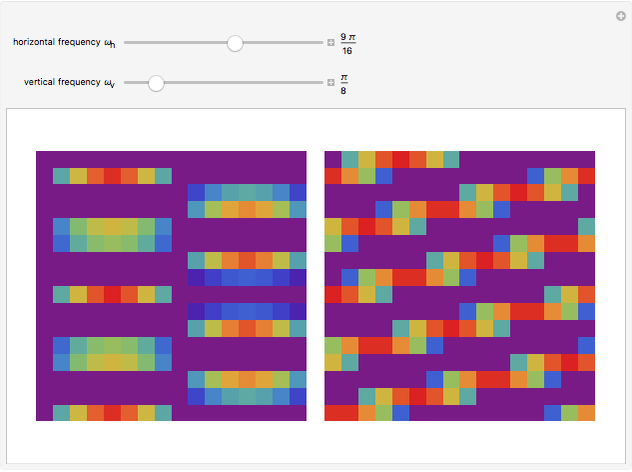
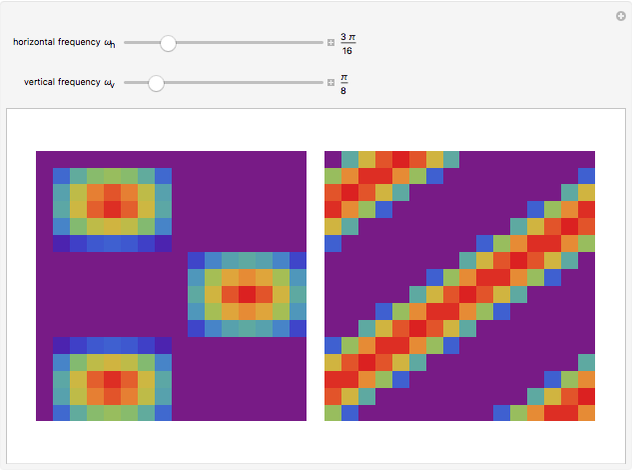
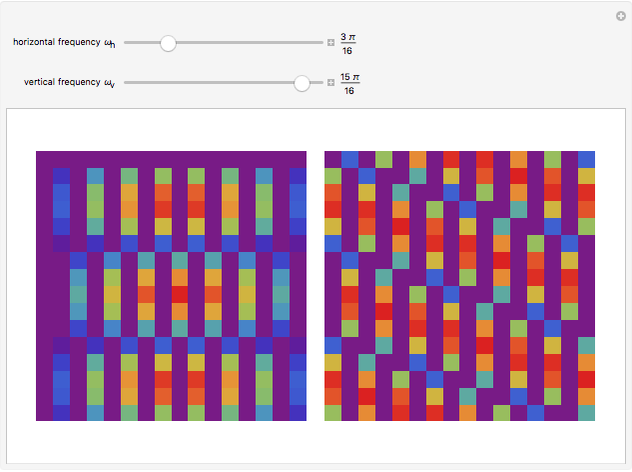
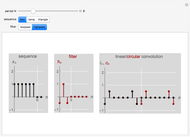
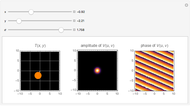
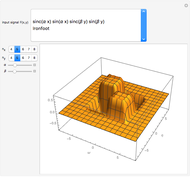
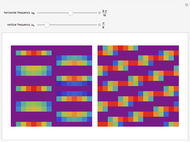
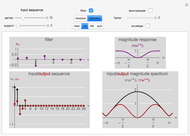
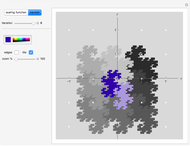
This Demonstration shows a separable 2D sinusoidal sequence (left) versus the nonseparable one (right) displayed as 16×16 images, with heights represented by colors.
[more]
Contributed by: Jelena Kovacevic (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The left figure (separable) is generated using
Reference
[1] M. Vetterli, J. Kovačević, and V. K. Goyal, Foundations of Signal Processing, Cambridge: Cambridge University Press, 2014. www.fourierandwavelets.org.
Permanent Citation