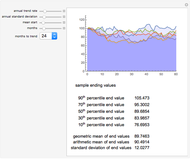
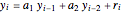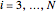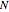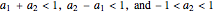Auto-Regressive Simulation (Second-Order)


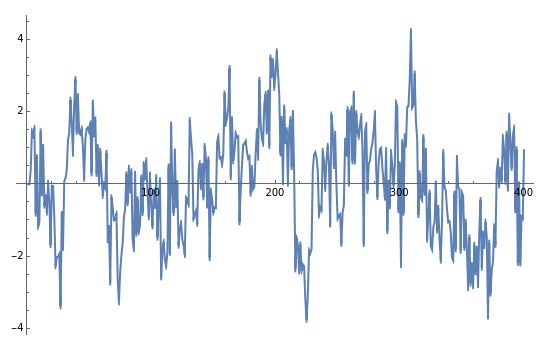
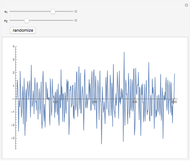
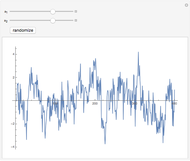
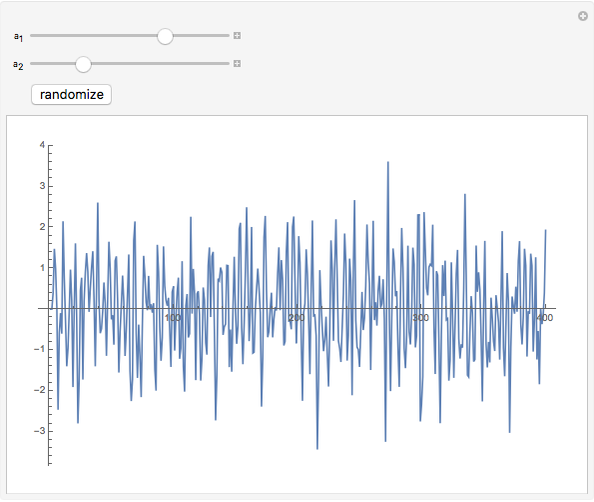
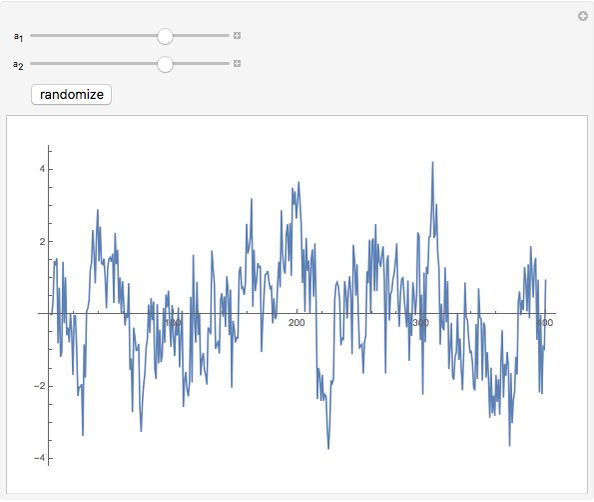
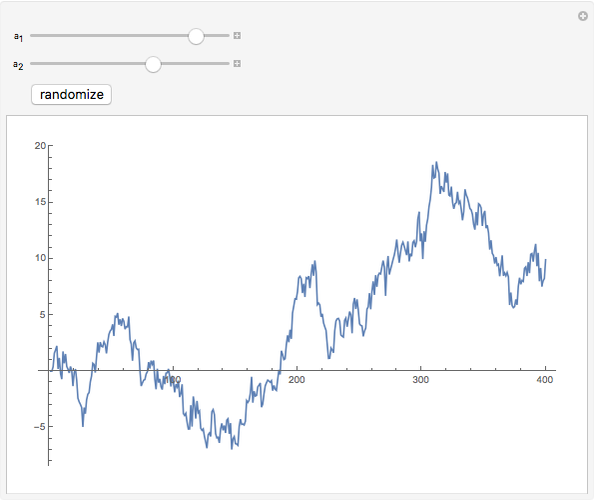
	This Demonstration shows realizations of a second-order auto-regressive (AR) process 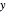, using the random variable drawn from a normal density with mean zero and variance unity. It is governed by the equation: (, where is the length of the series). The constants and are the auto-regressive constants. If , the series is stationary. A series of length 400 is created in every case.


	Contributed by: David von Seggern (University of Nevada)
	Show Initialization Code

The Demonstration is set such that the same random series of points is used no matter how the constants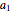

and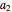

are varied. However, when the "randomize" button is pressed, a new random series will be generated and used. Keeping the random series identical allows the user to see exactly the effects on the AR series of changes in the two constants. If the constants

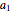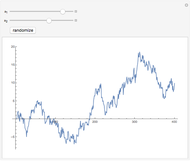
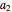do not meet the stationarity conditions, the series will diverge. The Demonstration is for a second-order process only. Additional AR terms would enable somewhat more complex series to be generated, but the differences from second-order processes would be difficult to ascertain.

For a detailed description of an AR process, see, for instance, G. M. Jenkins and D. G. Watts, Spectral Analysis and Its Applications, San Francisco: Holden-Day, 1968 or G. Box, G. M. Jenkins, and G. Reinsel, Time Series Analysis: Forecasting and Control, 3rd ed., Englewood Cliffs, NJ: Prentice-Hall, 1994.