Autothermal Reactor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
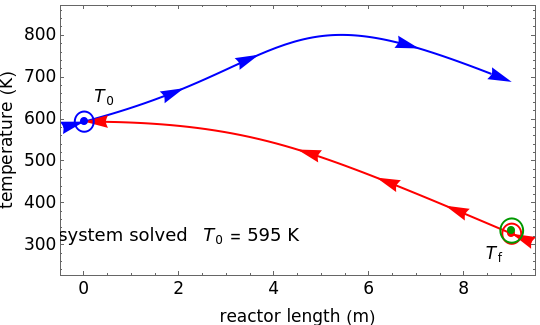
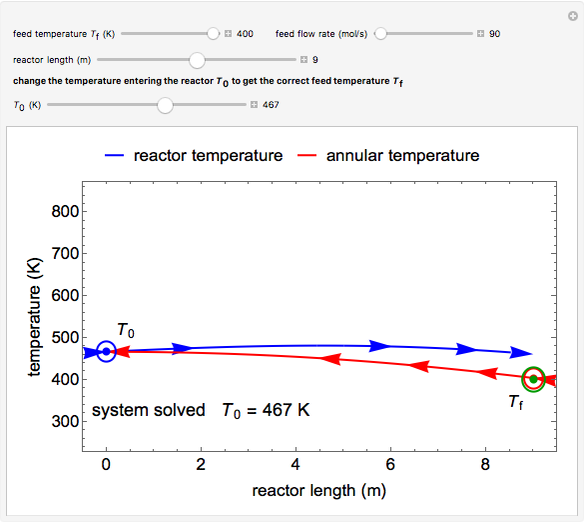
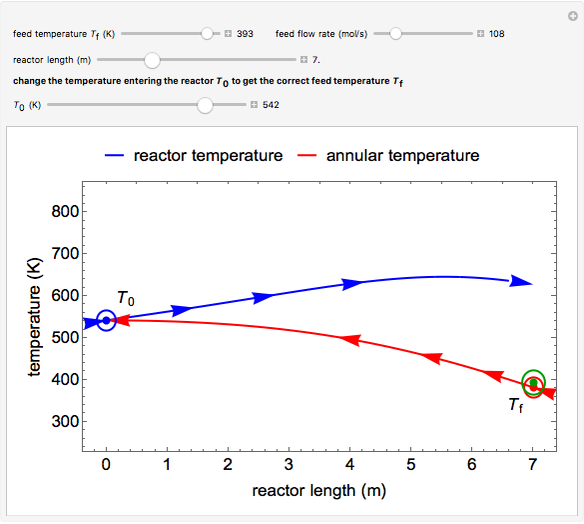
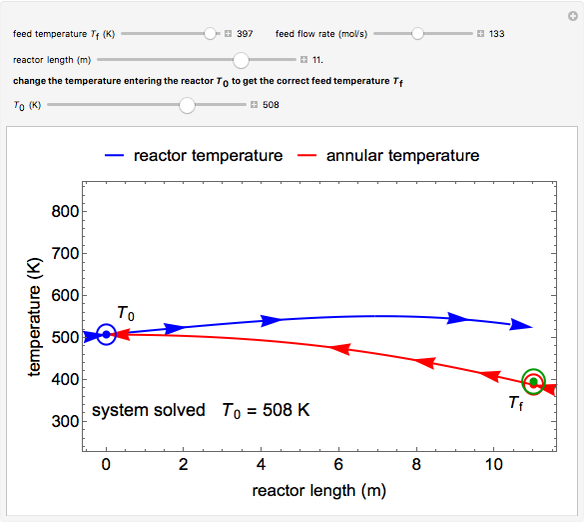
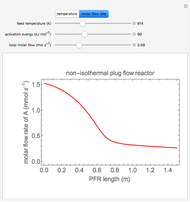
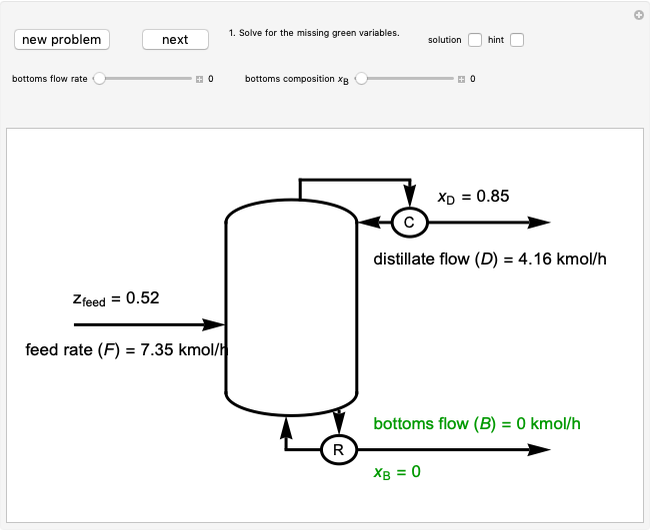
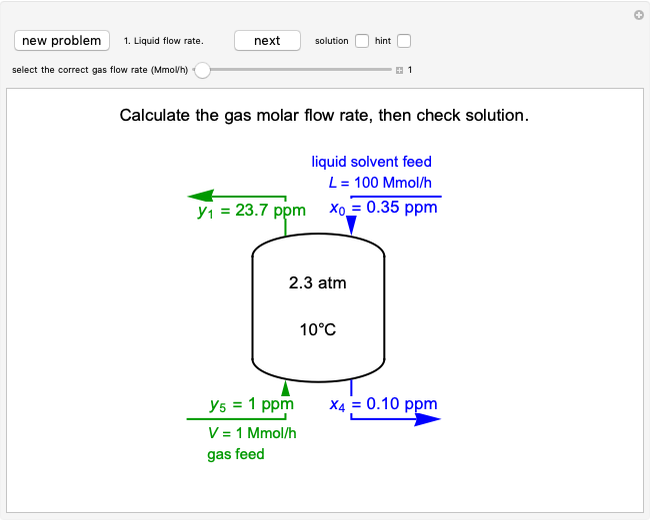
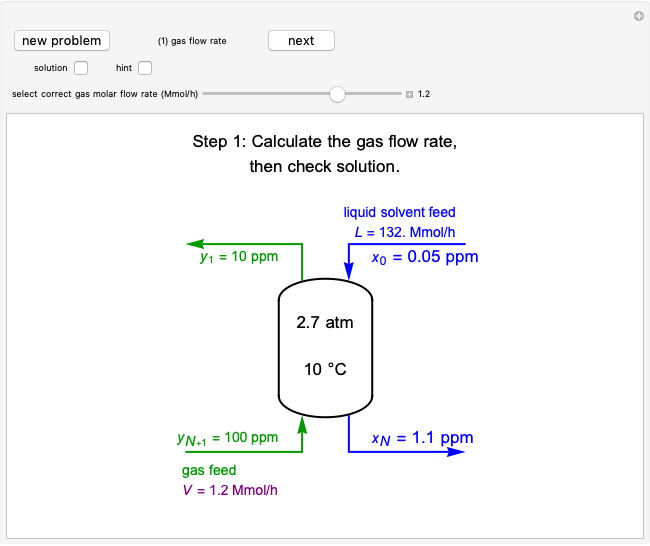
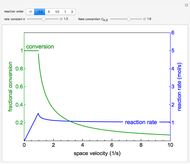
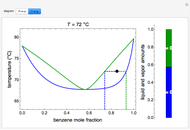
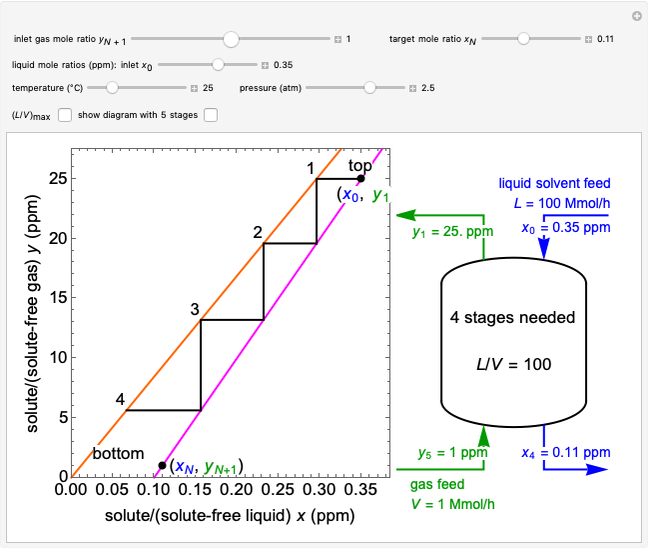
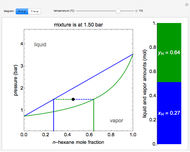
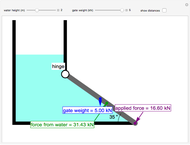
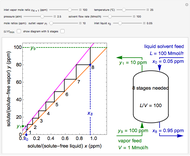
This autothermal reactor consists of two concentric tubes. The feed enters an annular region between the tubes at temperature 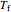 and flows from right to left. The reactants are at temperature
and flows from right to left. The reactants are at temperature 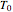 when they enter the inner tube, which is a packed catalyst bed, where they flow left to right. An exothermic reaction in the catalyst bed raises the gas temperature and heat transfers from the catalyst bed to preheat the gas in the annular region. To solve the ordinary differential equations (ODEs) that model this reactor, a shooting method is used; a value of
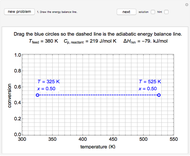
when they enter the inner tube, which is a packed catalyst bed, where they flow left to right. An exothermic reaction in the catalyst bed raises the gas temperature and heat transfers from the catalyst bed to preheat the gas in the annular region. To solve the ordinary differential equations (ODEs) that model this reactor, a shooting method is used; a value of 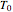 (the blue circle) is guessed and then changed until the correct value of
(the blue circle) is guessed and then changed until the correct value of 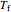 is obtained. This is done by moving the slider for
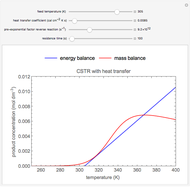
is obtained. This is done by moving the slider for 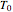 until the red circle is inside the green circle. Two reactor conditions are possible (two solutions to the mass and energy balances), one of which corresponds to essentially no reaction. Reactor startup determines which condition is obtained.
until the red circle is inside the green circle. Two reactor conditions are possible (two solutions to the mass and energy balances), one of which corresponds to essentially no reaction. Reactor startup determines which condition is obtained.
Contributed by: Rachael L. Baumann (July 2013)
With additional contributions by: John L. Falconer and Nick Bongiardina
Open content licensed under CC BY-NC-SA
Snapshots
Details
Material balance on packed bed:
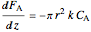 ,
,
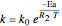 ,
,
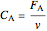 ,
,
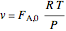 ,
,
where 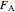 and
and 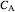 are the molar flow rate (mol/s) and concentration (
are the molar flow rate (mol/s) and concentration (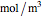 ) of
) of 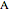 ,
,  is distance down the reactor (m),
is distance down the reactor (m),  is the cross-sectional radium of the reactor (m),
is the cross-sectional radium of the reactor (m),  is the rate constant (1/s),
is the rate constant (1/s), 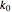 is a pre-exponential factor (1/s),
is a pre-exponential factor (1/s), 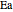 is activation energy (J/mol),
is activation energy (J/mol), 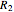 is the ideal gas constant (J/[mol K]),
is the ideal gas constant (J/[mol K]), 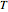 is temperature (K),
is temperature (K),  is volumetric flow rate (
is volumetric flow rate (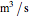 ),
), 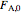 is the inlet molar flow rate of
is the inlet molar flow rate of 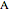 (mol/s),
(mol/s), 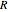 is the ideal gas constant (
is the ideal gas constant (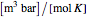 ), and
), and 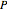 is pressure (bar).
is pressure (bar).
Energy balance on packed bed:
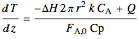 ,
,
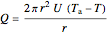 ,
,
where 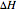 is heat of reaction (J/mol),
is heat of reaction (J/mol), 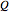 is heat transfer rate (J/s),
is heat transfer rate (J/s), 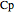 is mass heat capacity (J/[g K]),
is mass heat capacity (J/[g K]), 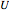 is the overall heat transfer coefficient (
is the overall heat transfer coefficient (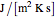 ),
), 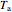 is the temperature of the annular region (K),
is the temperature of the annular region (K), 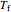 is the feed temperature to the reactor (K), and
is the feed temperature to the reactor (K), and 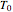 is the feed temperature to the packed bed (K).
is the feed temperature to the packed bed (K).
Energy balance on annular region:
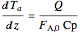 .
.
The sign of the heat transfer term in the annular region is negative because integration is opposite to the direction of flow.
For the solution in which the reaction rate is nonzero, the feed temperature in the annular region increases as the feed flows to the left and is heated by the packed bed. The temperature increases in the packed bed due to the exothermic reaction and some of the energy transfers to the feed gas in the annular region. As the reactant is used up, the temperature in the packed bed reaches a maximum and decreases as heat is transferred to the feed gas.
The screencast video at [2] shows how to use this Demonstration.
References
[1] J. G. Ekerdt and J. B. Rawlings, Chemical Reactor Analysis and Design Fundamentals, Madison, WI: Nob Hill Publishing, 2002 pp. 326–332.
[2] Autothermal Reactor. www.colorado.edu/learncheme/kinetics/AutothermalReactor.html.
Permanent Citation