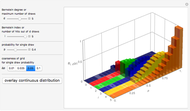
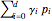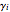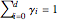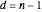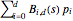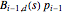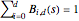Bernstein Polynomials and Convex Bézier Sums

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
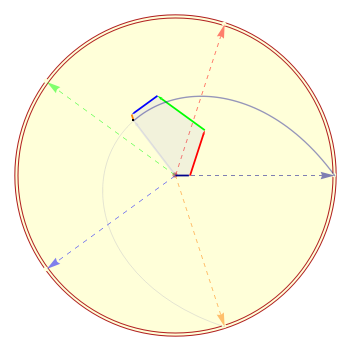
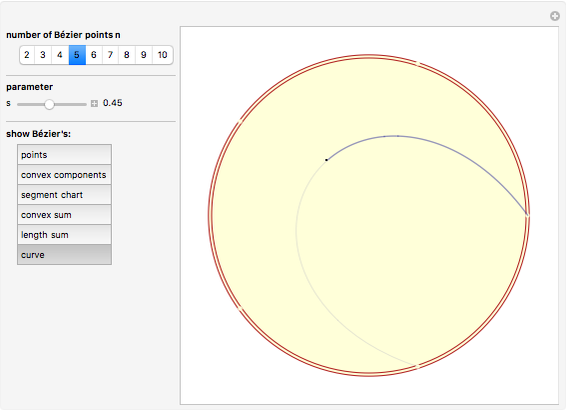
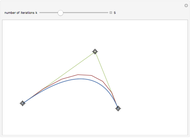
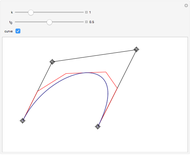
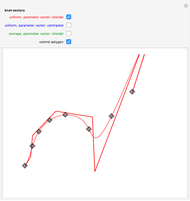
This Demonstration throws light on the fact that the points 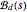 that form a basic Bézier curve are convex combinations of the Bézier points
that form a basic Bézier curve are convex combinations of the Bézier points 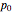 to
to 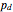 :
: 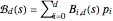 , where the coefficients
, where the coefficients 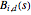 are just the
are just the 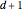 Bernstein polynomials of degree
Bernstein polynomials of degree  and
and  is a parameter running from 0 to 1.
is a parameter running from 0 to 1.
Contributed by: Ludwig Weingarten (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Bernstein polynomials, 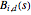 , are weighted multiples of
, are weighted multiples of  and
and  of the form
of the form 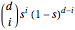 , where
, where  is the degree,
is the degree, 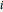 is the index running from 0 to
is the index running from 0 to  , and
, and 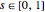 . So, for each degree
. So, for each degree  , there are
, there are 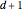 polynomial functions
polynomial functions 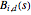 from
from 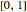 to
to 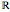 . The only zeros of these functions are 0 and 1; the index
. The only zeros of these functions are 0 and 1; the index 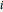 counts the multiplicity of the root at 0 and
counts the multiplicity of the root at 0 and 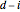 counts the multiplicity of the root at 1. In addition, they are positive in
counts the multiplicity of the root at 1. In addition, they are positive in 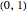 , nonnegative in [0,1] and, for each
, nonnegative in [0,1] and, for each  , they sum to the constant function 1 on
, they sum to the constant function 1 on 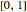 , so they constitute a partition of unity. This is why they can be used to build convex combinations.
, so they constitute a partition of unity. This is why they can be used to build convex combinations.
In Mathematica these polynomials are denoted as BernsteinBasis[d,i,s].
Thinking of the variable  as a parameter, a Bernstein vector of degree
as a parameter, a Bernstein vector of degree  and parameter
and parameter  can thus be defined as
can thus be defined as 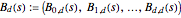 , a vector of functions from
, a vector of functions from 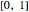 to
to 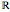 , with
, with 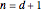 entries.
entries.
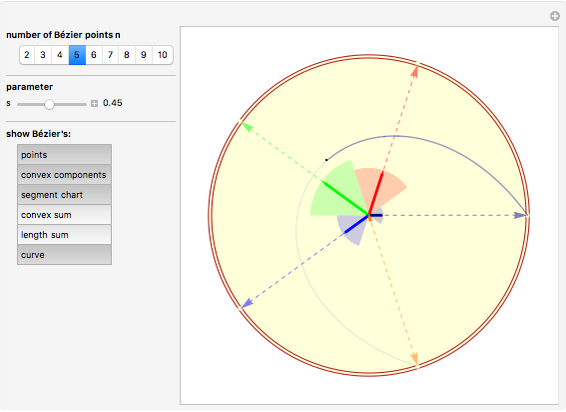
On the other hand, if the  roots of unity on the unit circle are
roots of unity on the unit circle are  , then for every parameter value
, then for every parameter value 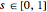 , the linear combinations
, the linear combinations 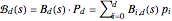 are a convex combination of the points
are a convex combination of the points 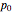 to
to 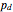 . They lie within the convex hull of
. They lie within the convex hull of 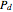 and thus within the unit circle.
and thus within the unit circle.
Regarded as a mapping from 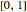 to the plane, these linear combinations
to the plane, these linear combinations 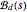 form a curve called the "basic Bézier curve of the points
form a curve called the "basic Bézier curve of the points 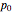 to
to 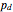 ". A component
". A component 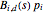 is called the "Bézier part of
is called the "Bézier part of 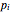 "; the combination
"; the combination 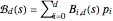 is also called the "Bézier sum of
is also called the "Bézier sum of 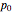 to
to 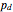 ".
".
Note: "basic" means that we are talking about polynomial curves, not piecewise polynomials!
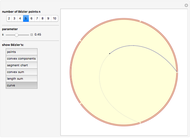
Snapshot 1: click the buttons one after the other; after any change mouse over the graphics to see explanations
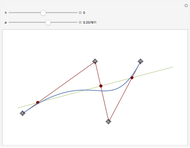
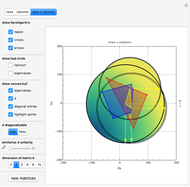
Snapshot 2: the convex components are shown underlined by the corresponding segment chart
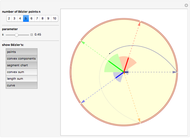
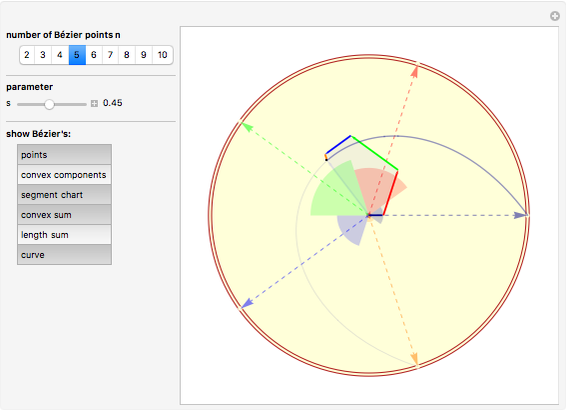
Snapshot 3: the convex sum and Bézier's polygon are shown, the length of its components indicated by the segment radius
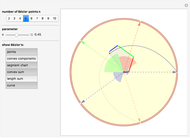
Snapshot 4: the convex sum and Bézier's polygon are shown, the length of its components indicated by the length sum
Permanent Citation