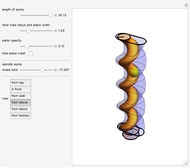
Bouncing Bob Pendulum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
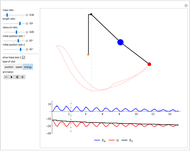
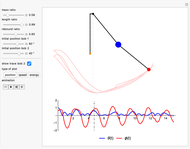
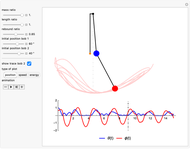
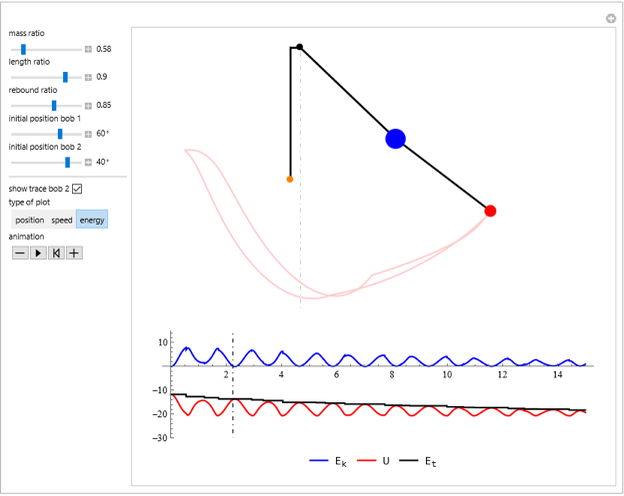
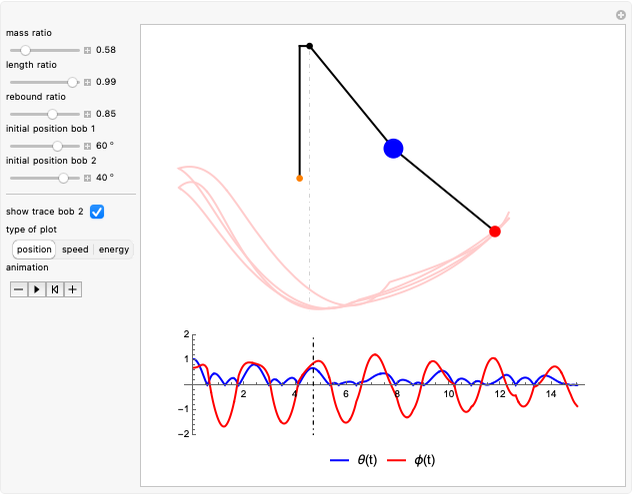
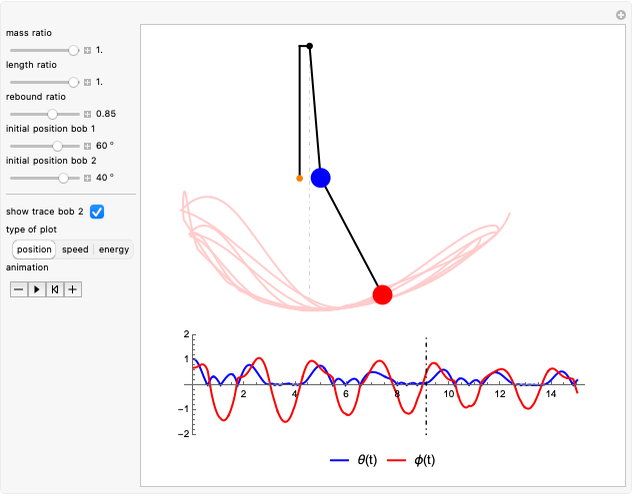
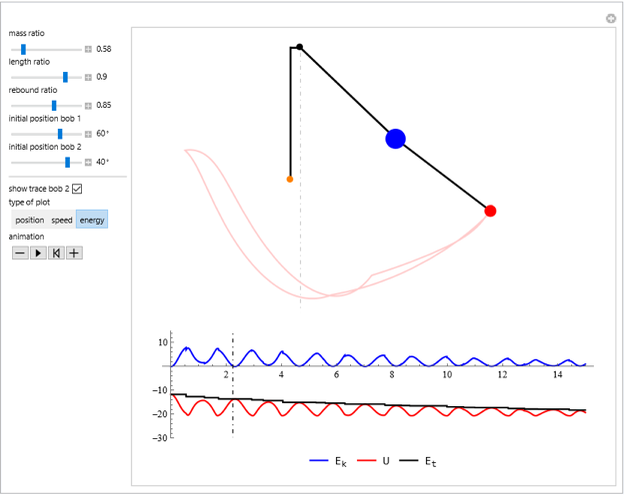
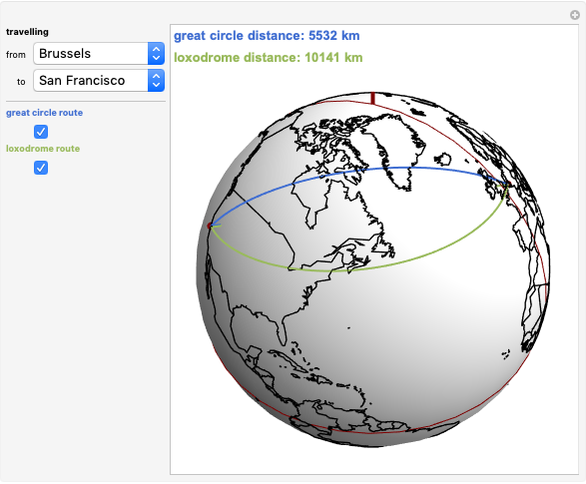
This Demonstration simulates the motion of a double pendulum with the upper bob bouncing back from an obstruction along the vertical axis.
[more]
Contributed by: Erik Mahieu (February 2024)
With additional contributions by: Franz Brandhuber
Open content licensed under CC BY-NC-SA
Snapshots
Details
In this Demonstration, the upper arm has both mass and length set to 1. The lower arm has mass 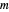 and length
and length  . The angular positions of the arms are
. The angular positions of the arms are 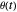 and
and 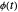 .
.
Lagrangian mechanics can be used to derive the equations of motion of the double pendulum. The potential energy and kinetic energy of the pendulum are
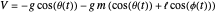 ,
,
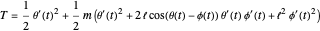 .
.
Adding the kinetic energy and subtracting the potential energy gives the Lagrangian, 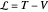 .
.
Substituting this into the Euler–Lagrange equations results in the equations of motion:
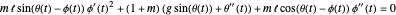 ,
,
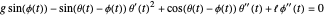 .
.
During the solution of these differential equations, the event θ[t]⩵0 triggers WhenEvent, resulting in an action for each of the angular positions of the bobs: 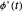 is replaced by
is replaced by 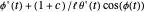 and
and 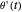 is replaced by
is replaced by  , where
, where  is the rebound ratio.
is the rebound ratio.
The formula for the rebound actions was taken from [1].
Snapshot 3 shows that for a 100% elastic impact (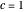 ), the total energy
), the total energy 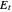 stays constant during the animation.
stays constant during the animation.
Reference
[1] S. Timoshenko and D. H. Young, "Lagrangian Equations for Impulsive Forces," Advanced Dynamics, New York: McGraw-Hill, 1948 pp. 225–230.
Permanent Citation