Celestial Navigation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
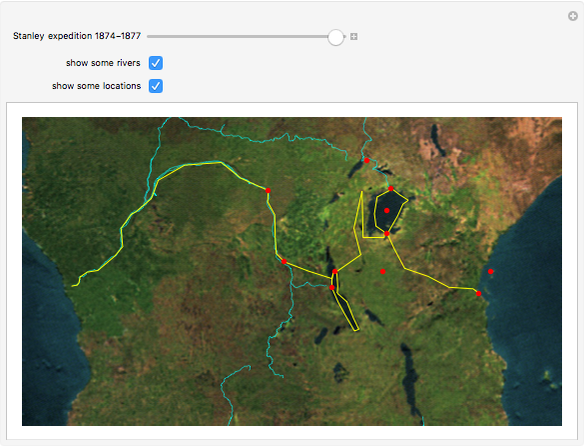
This Demonstration illustrates the basic principle behind the practice of celestial navigation.
[more]
Contributed by: Hans Milton (March 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
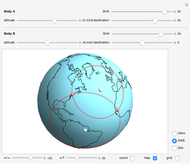
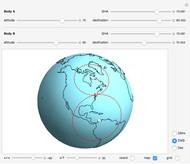
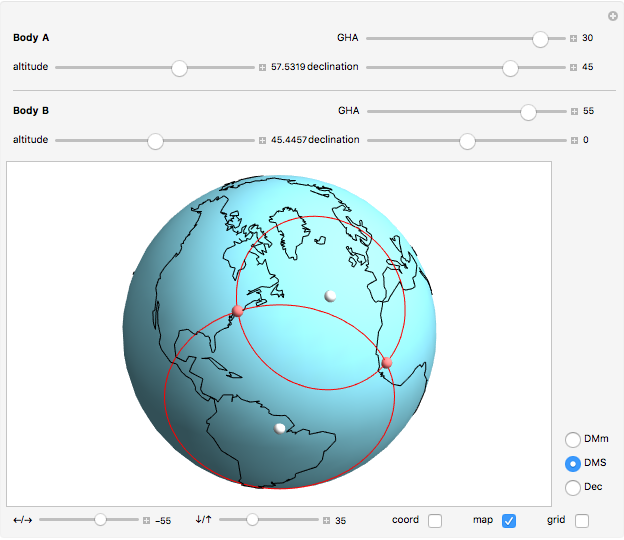
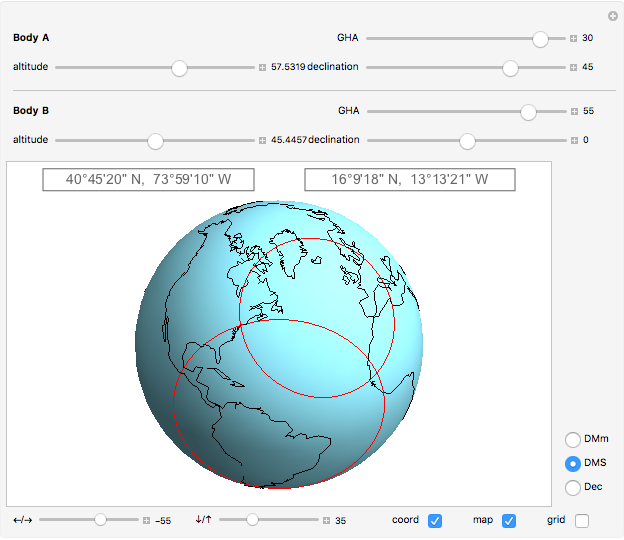
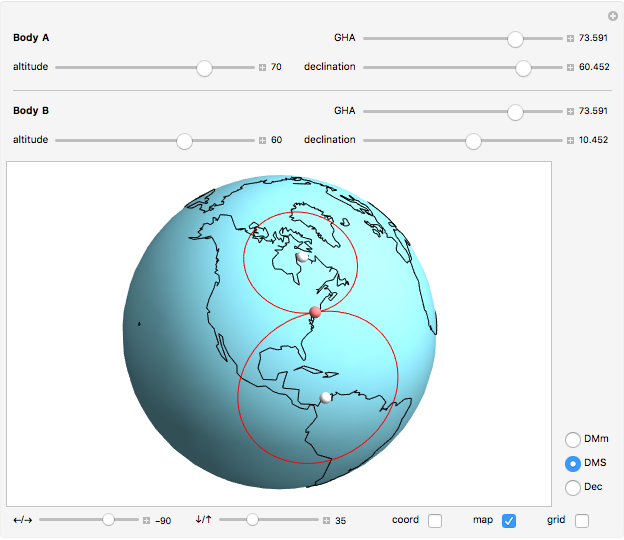
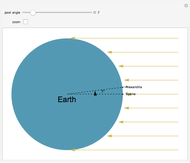
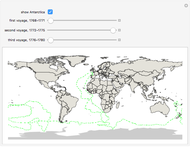
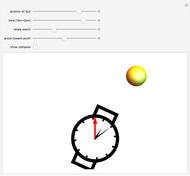
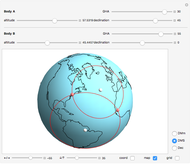
The substellar point of a celestial body is the point on the surface of the Earth where a line drawn from the body to the center of the Earth penetrates the Earth's surface. Rephrased, it is the position on Earth where the body in question is directly overhead.
Nautical almanacs are regularly published in print and online. They tabulate the substellar points for celestial bodies, as they change with date and time of day.
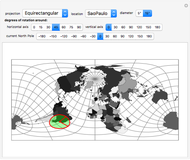
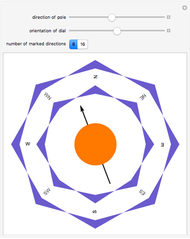
In general, the longitudinal coordinate in the almanacs is given in Greenwich hour angle, GHA, measured in degrees west of Greenwich. In the range from 0 to 360. This is in contrast to the common map longitude measurement that is in the range 180° west to 180° east. With 0° at the Greenwich meridian.
For a star, the longitudinal coordinate might be expressed in sidereal hour angle, SHA. The corresponding GHA is found by adding the star's SHA to the GHA of the first point in Aries.
The latitudinal coordinate is the same in the almanacs as on the map; it is measured in the range from 90° south to 90° north.
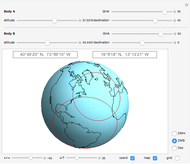
The most common notation for angles in the almanacs is in degrees with decimal arc minutes. In the Demonstration, this notation is selected by the radio button DMm.
Two other notations for angles can also be selected: DMS gives degrees/minutes/seconds, and Dec gives decimal degrees.
For an insight into the actual practical methods of aerial celestial navigation as it was done in the middle of the last century, see [4].
References
[1] Online Almanac: reednavigation.com/lunars/nadata_v5.html
[2] Printed Almanacs: aa.usno.navy.mil/publications/
[3] Latitude and Longitude of a Point: itouchmap.com/latlong.html
[4] W. Hadel, Celestial Navigation: A Problem Manual, 1st. ed, New York: McGraw Hill, 1944.
Permanent Citation
"Celestial Navigation"
http://demonstrations.wolfram.com/CelestialNavigation/
Wolfram Demonstrations Project
Published: March 20 2013