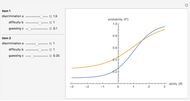
Comparing the Normal Ogive and Logistic Item Characteristic Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
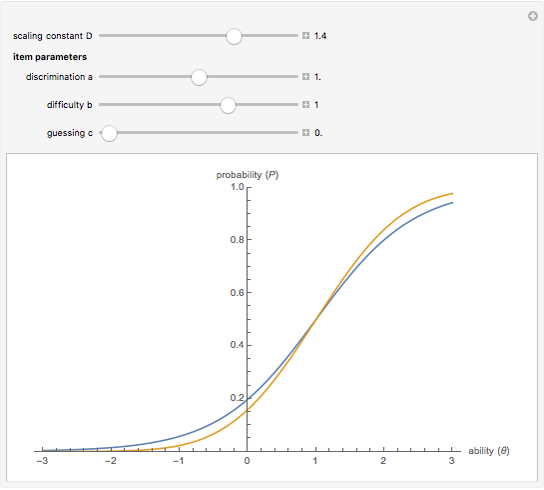
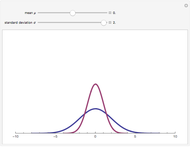
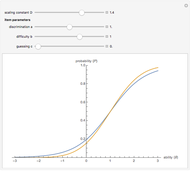
In item response theory, the relationship between a latent ability ( ) and the probability of a correct response (
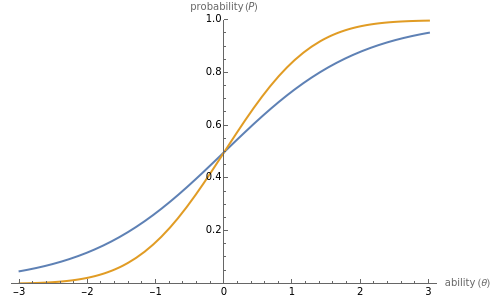
) and the probability of a correct response (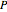 ) on a test item is modelled by an item characteristic curve. This Demonstration plots the item characteristic curve of a single dichotomous item under two different models: the normal ogive model and the logistic model. The parameters
) on a test item is modelled by an item characteristic curve. This Demonstration plots the item characteristic curve of a single dichotomous item under two different models: the normal ogive model and the logistic model. The parameters  ,
,  , and
, and  represent item properties related to discrimination, difficulty, and guessing. The constant
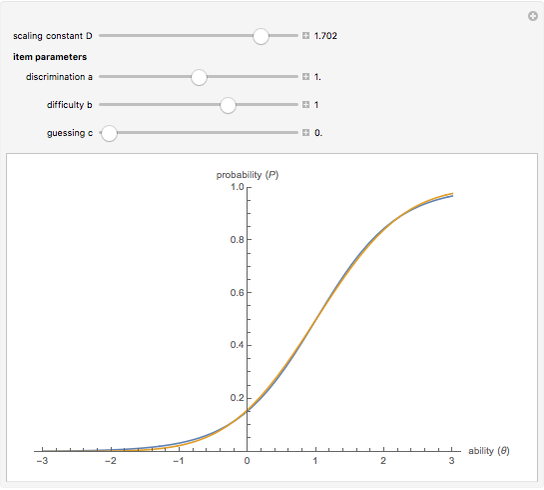
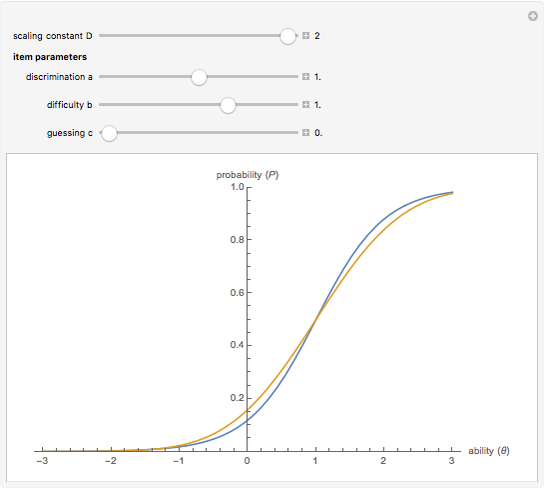
represent item properties related to discrimination, difficulty, and guessing. The constant 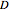 is used to scale the logistic curve. Notice that the two curves are nearly identical when
is used to scale the logistic curve. Notice that the two curves are nearly identical when 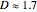 .
.
Contributed by: Vincent Kieftenbeld (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The probability that a person with ability level  gives a correct response (
gives a correct response (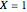 ) to an item with discrimination parameter
) to an item with discrimination parameter  , difficulty parameter
, difficulty parameter  , and pseudo-guessing parameter
, and pseudo-guessing parameter  is modelled in the normal ogive model as
is modelled in the normal ogive model as
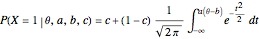 .
.
Alternatively, in the three-parameter logistic model,
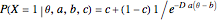 .
.
The constant D is used to scale the logistic curve and represents the relationship between logits and probits. When 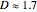 , the models agree closely; that is, 1 logit is approximately equal to 1.7 probit. In fact,
, the models agree closely; that is, 1 logit is approximately equal to 1.7 probit. In fact, 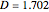 minimizes the maximum difference between the normal ogive and logistic curves.
minimizes the maximum difference between the normal ogive and logistic curves.
Reference:
G. Camilli, "Origin of the Scaling Constant d=1.7 in Item Response Theory," Journal of Educational and Behavioral Statistics, 19(3), 1994 pp. 293–295.
Permanent Citation