Engineering Dynamics: Tip or Slip?

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
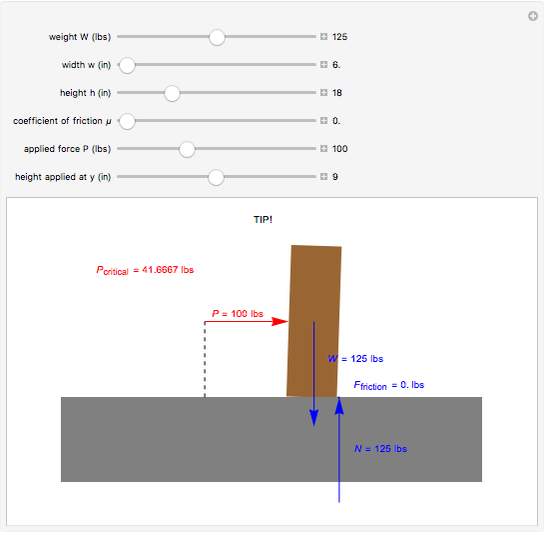
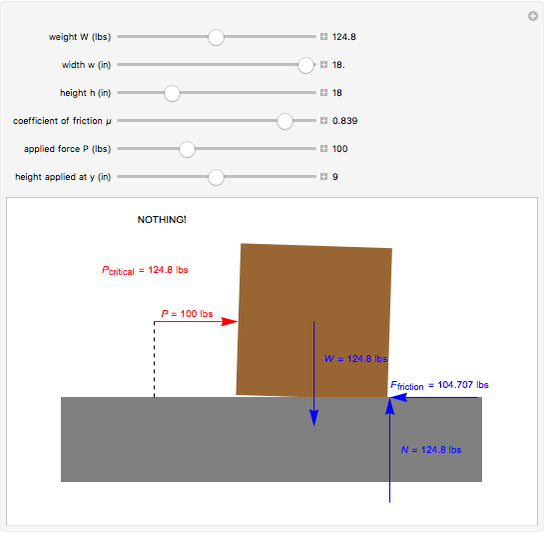
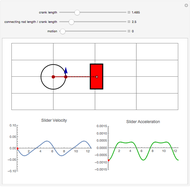
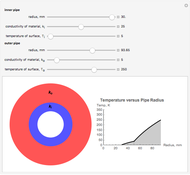
This Demonstration determines if an object slips across a surface or tips over. By combining a free-body diagram with the basic principles of engineering dynamics, it is possible to determine the conditions under which the object will tip over instead of slipping along the surface.
Contributed by: Sara McCaslin and Fredericka Brown (July 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
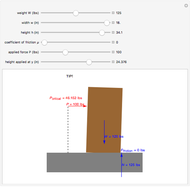
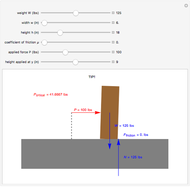
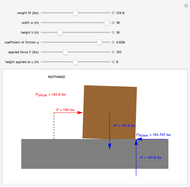
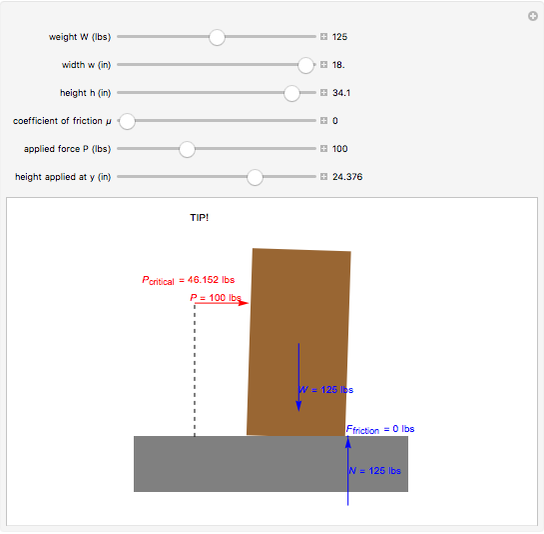
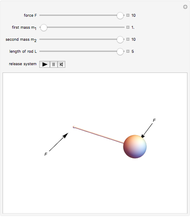
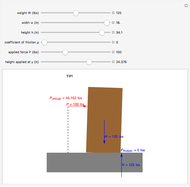
This Demonstration shows a free-body diagram of an object as it is just about to tip over (impending motion). In that case, the normal force  acts at the far right instead of along the centerline of the object. Friction acts at the base of the object in a direction opposing the motion of the object and along the surface. The weight
acts at the far right instead of along the centerline of the object. Friction acts at the base of the object in a direction opposing the motion of the object and along the surface. The weight 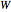 acts downward through the center of gravity.
acts downward through the center of gravity.
We know that the object does not move vertically, thus, by addition of forces, 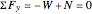 , that is, the normal force acting on the object is equal to its weight (
, that is, the normal force acting on the object is equal to its weight ( ). The equation for friction is
). The equation for friction is  , where
, where  is the coefficient of friction between the object and the surface (no friction corresponds to
is the coefficient of friction between the object and the surface (no friction corresponds to  ). The next step is to determine the value of
). The next step is to determine the value of 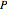 that will cause the object to tip over. For this, we take the sum of the moments about the lower-right corner of the object:
that will cause the object to tip over. For this, we take the sum of the moments about the lower-right corner of the object: 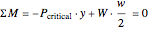 , giving
, giving 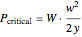 . Thus the object cannot slide across the surface as long as the value of
. Thus the object cannot slide across the surface as long as the value of 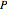 is less than
is less than 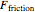 . For the object to slide across the floor without tipping,
. For the object to slide across the floor without tipping, 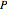 must lie in the range
must lie in the range 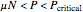 .
.
The user can vary these values: object width 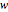 , height
, height  , and weight
, and weight 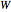 ; the coefficient of friction
; the coefficient of friction  between the object and the surface; the applied force,
between the object and the surface; the applied force, 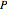 , and the height
, and the height 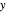 at which the force is applied.
at which the force is applied.
What results would you expect if you were to try moving the box across ice (hint: 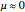 )? Does the force required for tipping increase or decrease as the force is applied closer to the top? Which is harder to tip over: a wide box or a narrow box? Does friction have any affect on whether the object will slip or tip? The answers to all these questions can be confirmed by experimenting with this Demonstration.
)? Does the force required for tipping increase or decrease as the force is applied closer to the top? Which is harder to tip over: a wide box or a narrow box? Does friction have any affect on whether the object will slip or tip? The answers to all these questions can be confirmed by experimenting with this Demonstration.
Reference
[1] W. F. Riley and L. D. Sturges, Engineering Mechanics: Dynamics, 2nd ed., New York: John Wiley and Sons, 1995.
Permanent Citation