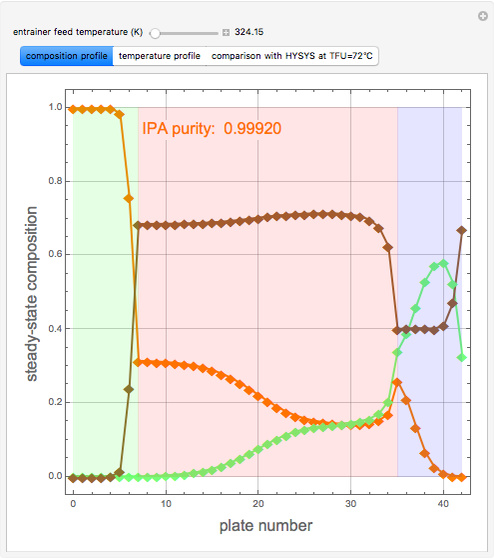
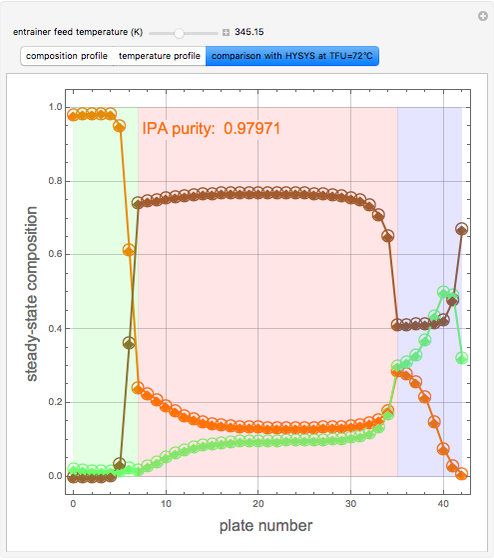
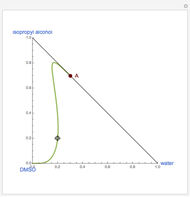
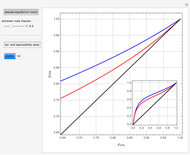
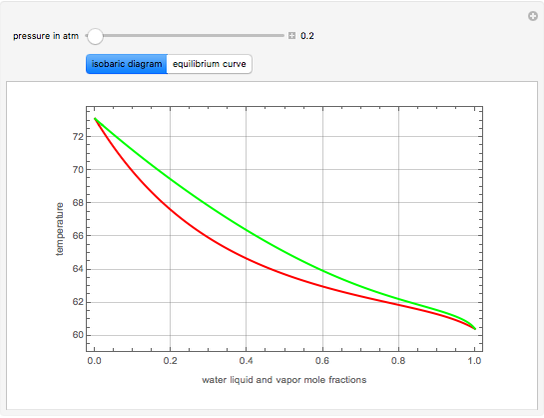
Extractive Distillation of an Azeotropic Mixture of Isopropyl Alcohol and Water: Effect of Entrainer Feed Temperature

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
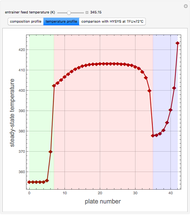
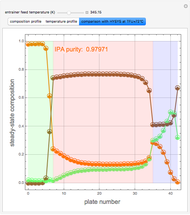
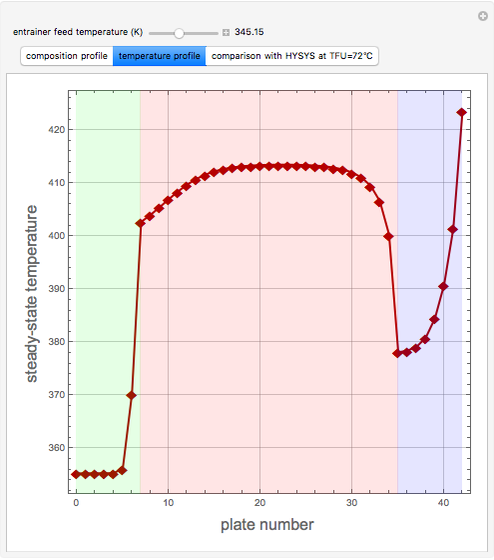
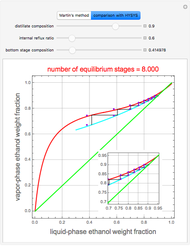
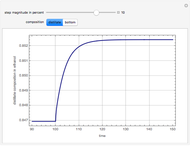
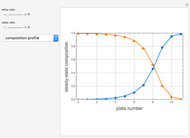
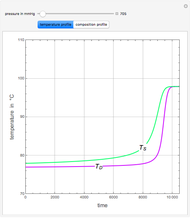
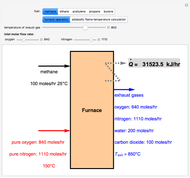
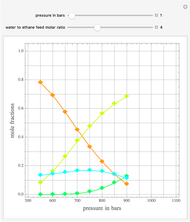
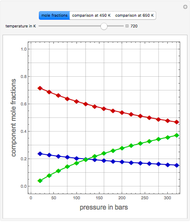
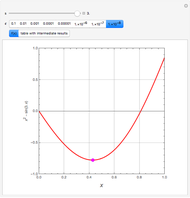
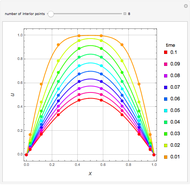
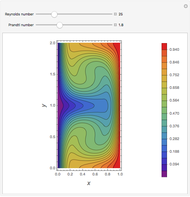
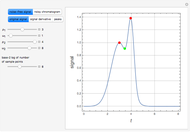
Extractive distillation is one of several methods that can be used to separate an azeotropic mixture. In extractive distillation a third component, called an entrainer, is added to the mixture to break the azeotrope. This Demonstration examines the effect of entrainer temperature on the efficiency of separation [1,3].
[more]
Contributed by: Housam Binous, Naim Faqir, Adamu Sagir, and Brian G. Higgins (November 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Expressions for pure component vapor and liquid enthalpies were adapted from Aspen HYSYS.
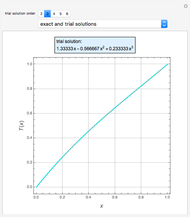
The mixture is assumed to obey the modified Raoult's law and activity coefficients are predicted using the Wilson model [4].
References
[1] M. F. Doherty and M. F. Malone, Conceptual Design of Distillation Systems, Boston: McGraw-Hill, 2001.
[2] E. J. Henley and J. D. Seader, Equilibrium-Stage Separation Operations in Chemical Engineering, New York: Wiley, 1981.
[3] W. L. Luyben and I.-L. Chien, Design and Control of Distillation Systems for Separating Azeotropes, Hoboken, NJ: Wiley, 2010.
[4] G. M. Wilson, "Vapor-Liquid Equilibrium XI: A New Expression for the Excess Free Energy of Mixing," Journal of the American Chemical Society, 86(2), 1964 pp. 127–130.