Fraction Tree and Continued Fractions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
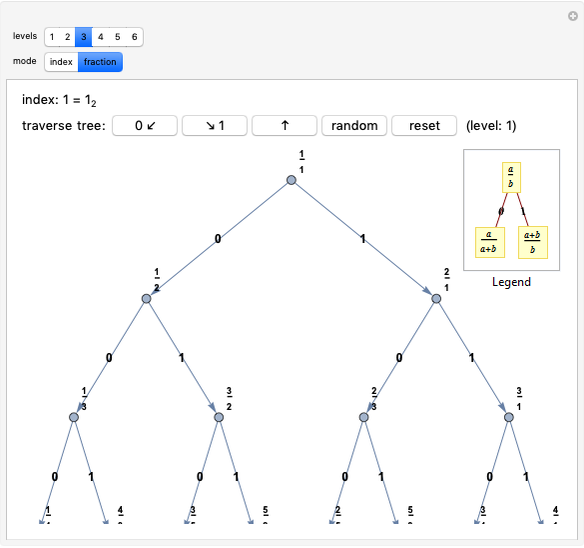
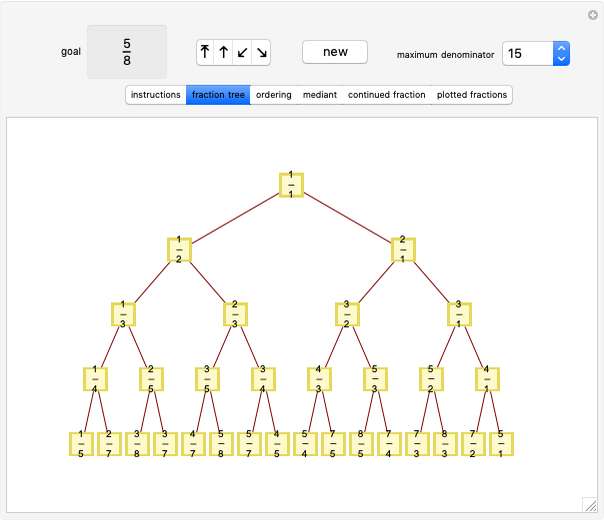
This Demonstration is a game for exploring connections between the Stern–Brocot tree and continued fractions.
[more]
Contributed by: David W. Carraher (March 2011)
(TERC)
Open content licensed under CC BY-NC-SA
Snapshots
Details
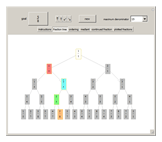
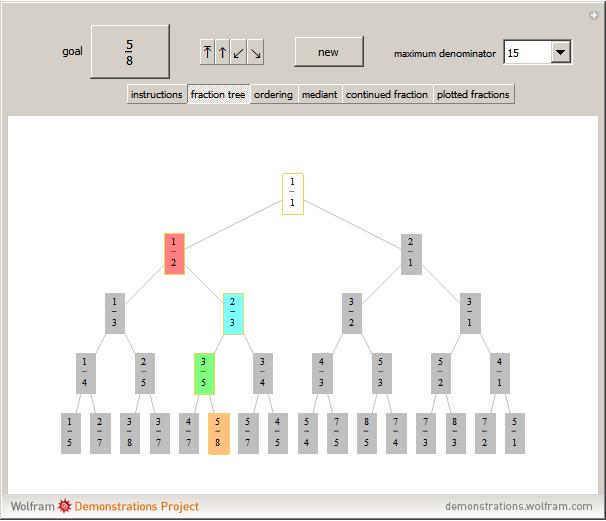
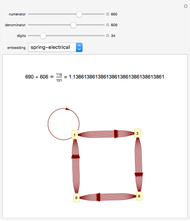
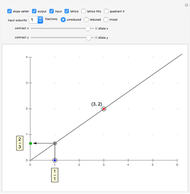
Snapshot 1: The fraction 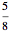 has been reached in the Stern–Brocot tree. It is possible to display up to 20 levels on the screen. Beyond five levels it is easier to keep track of the order of fractions using the "ordering" tab.
has been reached in the Stern–Brocot tree. It is possible to display up to 20 levels on the screen. Beyond five levels it is easier to keep track of the order of fractions using the "ordering" tab.
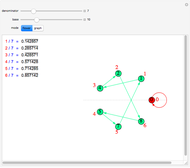
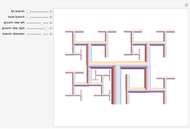
Snapshot 2: The same solution 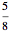 is shown in the order of the fractions visited. The ordering corresponds to collapsing the Stern–Brocot path onto a single dimension. The solution was reached by turning left, right, left, right.
is shown in the order of the fractions visited. The ordering corresponds to collapsing the Stern–Brocot path onto a single dimension. The solution was reached by turning left, right, left, right.
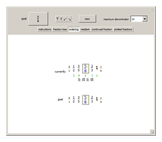
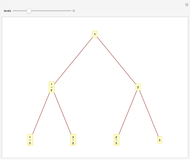
Snapshot 3: The fraction 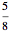 is shown as the mediant of
is shown as the mediant of  and
and  ; it was produced by summing the parents' numerators to produce the numerator of the mediant and summing the parents' denominators to produce the denominator of the mediant. This method, although incorrect as a way to add fractions, is the very way to produce a mediant. The mediant always lies between the parent fractions.
; it was produced by summing the parents' numerators to produce the numerator of the mediant and summing the parents' denominators to produce the denominator of the mediant. This method, although incorrect as a way to add fractions, is the very way to produce a mediant. The mediant always lies between the parent fractions.
Snapshot 4: Click the "continued fraction" tab to keep track of turns in the tree and to show how the continued fraction is built up from partial quotients.
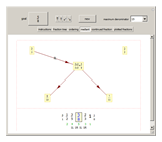
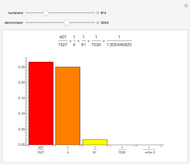
Snapshot 5: Click the "plotted fractions" tab to show how the fractions converge (or not) on the goal fraction. In the snapshot, the current slope is  ; the desired slope is
; the desired slope is 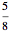 . All visited fractions, not only the convergents, are displayed in the plot.
. All visited fractions, not only the convergents, are displayed in the plot.
This Demonstration was developed under the auspices of the Poincaré Institute for Mathematics Education at Tufts University and TERC, an NSF-funded Math and Science Partnership project (NSF MSP DUE-0962863).
References
[1] R. L. Graham, D. E. Knuth, and O. Patashnik, Concrete Mathematics: A Foundation for Computer Science, Reading, MA: Addison–Wesley, 1994.
[2] H. M. Stark. "Number Theory from a Continued Fractions Viewpoint," An Introduction to Number Theory, Cambridge, MA: MIT Press, 1970 pp. 181–256.
Permanent Citation