Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Heat Capacity of Solids in the Debye Approximation

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

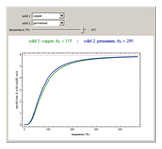
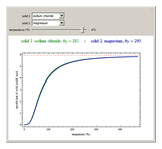
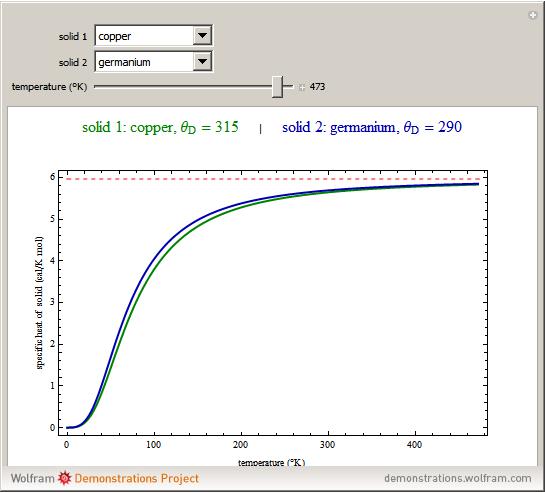
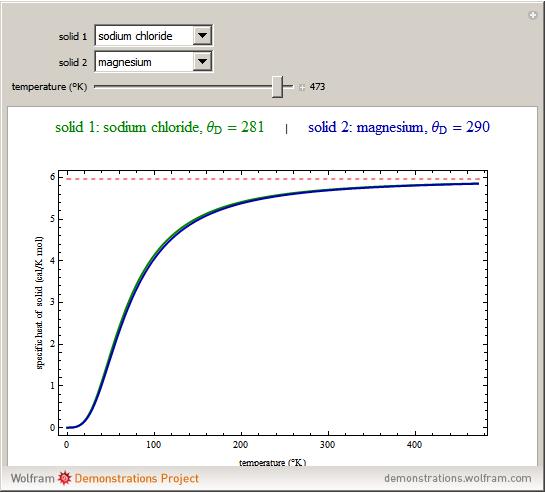
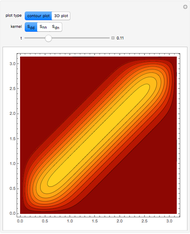
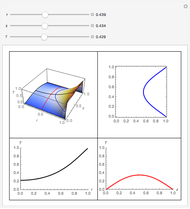
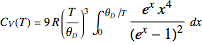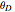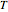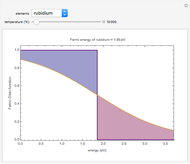
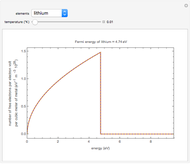
The value of the classical molar heat capacity , depends on temperature. In the Debye approximation, it is given by , where is the Debye temperature of the solid, is the absolute temperature, and 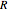is the gas constant. This Demonstration shows the variation of the specific heat of solids with temperature of representative solids according to the Debye theory.

Contributed by: Kallol Das (St. Aloysius College, Jabalpur, India) (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The dashed red line is the value of the molar heat capacity 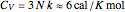as given by the Dulong–Petit law. The classical theory for the specific heat of solids does not explain the decrease of specific heat at low temperatures. The physical models of the specific heat curves as given by Einstein and subsequently by Debye employed the quantum theory and agreed well with experiment.

The Debye model details and the Debye temperature of solids are taken from A. J. Dekker, Solid State Physics, New Delhi: Macmillan India Limited, 2007.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send