Wolfram Research

Mathematica MathWorld Wolfram Science More »

HOME

Launching a Rocket


	The launch of a spacecraft is fundamental to all space activity. As a rocket flies it loses mass, because most of its mass is fuel (pure hydrogen and oxygen) that provides the propulsive force. This Demonstration shows the dynamics of an ideal rocket from launch time to measured burn-out time, based on Newton's laws and Tsiolkovsky's rocket equation. Specify the rocket parameters and launch with the trigger.


	Contributed by: Frederick Wu

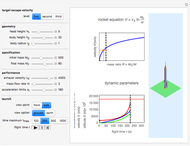
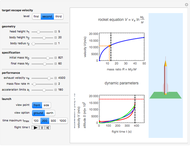
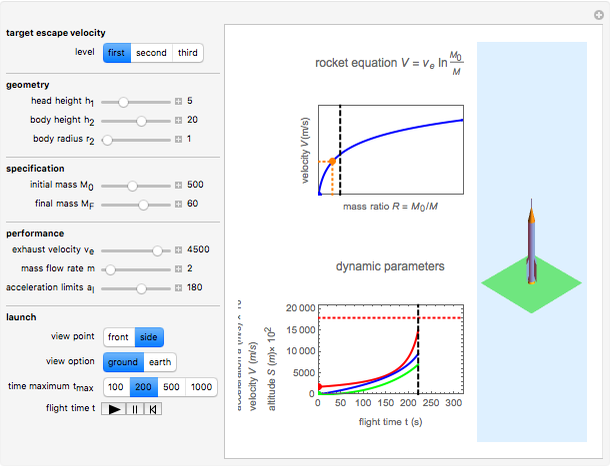
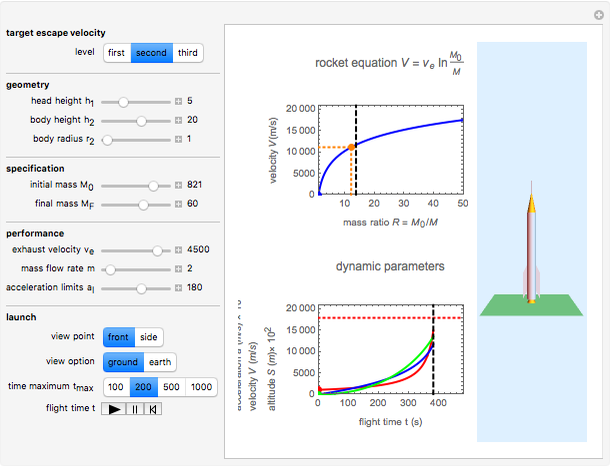
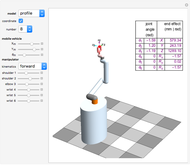
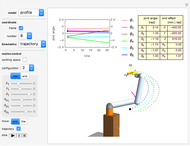
Graphic, top right: Tsiolkovsky's rocket equation, which defines the relationship between exhaust velocity and mass ratio

Graphic, bottom right: rocket dynamic parameters of acceleration, velocity, altitude and burn-out time

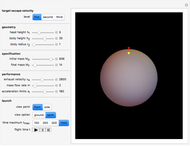
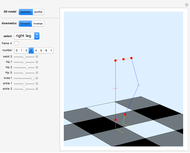
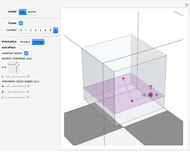
Graphic, left: 3D rocket dynamic launch model with altitude function control

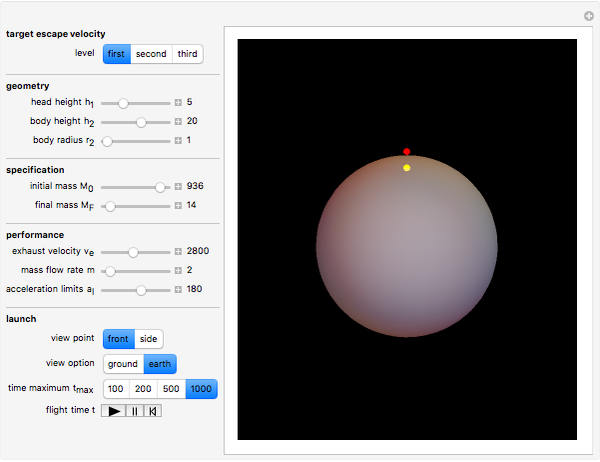
Snapshot 1: ideal rocket specification that surpasses first escape velocity

Snapshot 2: ideal rocket specification that surpasses second escape velocity

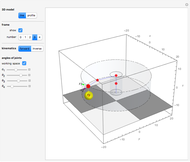
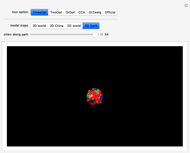
Snapshot 3: 3D Earth scale model, with the launch site (yellow) and rocket altitude (red)

simplified assumptions:

1. gravity and aerodynamic drag effects are neglected

2. single stage rocket, initial velocity is zero

3. vertical launch or pitch angle is 90°

4. a constant exhaust velocity

5. a constant mass flow rate

governing equations:

1. Tsiolkovsky's rocket equation or rocket velocity: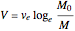

2. mass flow rate: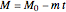

3. maximum flight time or fuel burn-out time: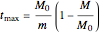

4. rocket altitude: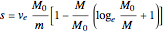

5. rocket acceleration: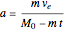

, from

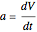and above governing equations 1 and 2

symbols:

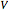is the rocket velocity.

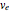is the efficient exhaust velocity, constrained within a range 2500-4500

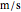, using today's liquid-fueled rocket chemical technology.

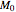is the initial rocket mass.

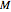is the current or final rocket mass;

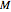decreases during flight until all the liquid fuel is burned out.

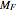is the final rocket mass, usually regarded as payload.

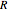is the mass ratio,

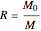, which is usually in the range from 3 to 8; 14 is difficult to achieve.

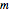is the mass flow rate, which depends on rocket engine design and specification; it indicates the rate at which the mass of the rocket is decreasing. Also called "specific impulse".

is the rocket flight time,

, which is the fuel burn-out time or the maximum flight time.

is the rocket acceleration. It is difficult for the human body to withstand high acceleration; 15-20 G is the maximum tolerance limit. (1 G is the acceleration due to gravity.)

References:

J. Peraire, "Variable Mass Systems: The Rocket Equation," MIT OpenCourseWare, 2004.

M. J. L. Turner, "Newton's Third Law and the Rocket Equation," Rocket and Spacecraft Propulsion, 2nd ed., New York: Springer, 2005 pp. 14–17.

M. J. L. Turner, "Launch Vehicle Dynamics," Rocket and Spacecraft Propulsion, 2nd ed., New York: Springer, 2005 pp. 115–144.

M. Voshell, "High Acceleration and the Human Body," 2004.

Escape Velocity (ScienceWorld)

Newton's Laws (ScienceWorld)

Newton's Second Law (ScienceWorld)

Newton's Third Law (ScienceWorld)

Rocket Equation (ScienceWorld)

Tsiolkovsky, Konstantin (1857-1935) (ScienceWorld)

"Launching a Rocket" from The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/LaunchingARocket/

Contributed by: Frederick Wu

Report an issue »

Interact with Demonstrations using the latest version of the free Mathematica Player—Download Now

Browse all topics

Browse all education topics

	Source page:
	Email	Name (optional)
	Occupation (optional)	Organization (optional)
	I use Mathematica often occasionally never
	Country (optional) Remember me
	Note: Please do not include anything you consider confidential or proprietary. Your message and contact information may be shared with the author of any specific Demonstration for which you give feedback, but will not otherwise be published or distributed. Privacy Policy »

Wolfram Research

Site Index

RSS

Atom