Linear Momentum Balance in Aerodynamic Thrust

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
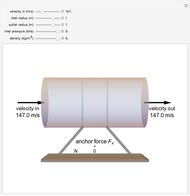
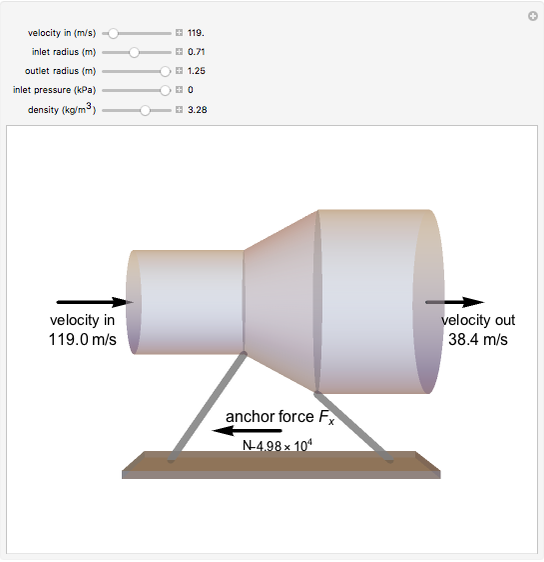
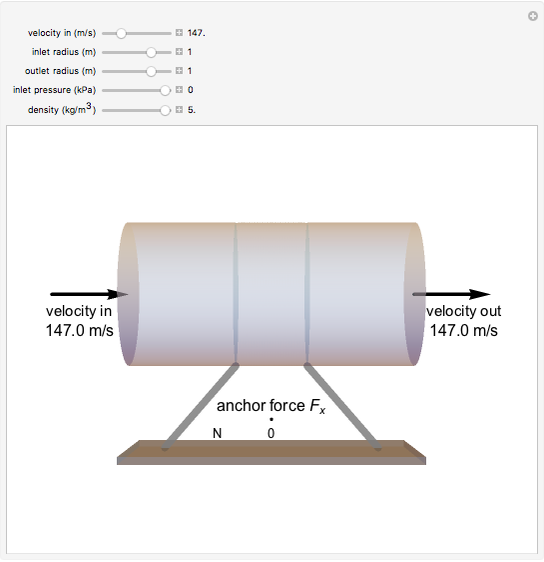
The force generated by a jet engine on a static thrust stand is determined using Newton's second law of motion. For a fixed, nondeforming control volume with uniform and steady flow, the sum of the forces is equal to the net rate of linear momentum flow through each control surface. Use sliders to change inlet and outlet radii, inlet velocity and inlet pressure. The anchoring force 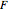 is the force to keep the jet engine stationary. The inlet and outlet pressures are gage pressures (
is the force to keep the jet engine stationary. The inlet and outlet pressures are gage pressures (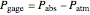 ).
).
Contributed by: Michael Wrobel and Ryan Hollenbaugh (October 2013)
Additional contributions by: Rachael L. Baumann, Garret D. Nicodemus and Nick Bongiardina
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The linear momentum balance for a nondeforming, stationary control volume is:
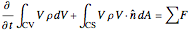 .
.
Since the flow is steady, the momentum balance simplifies to:
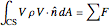 ,
,
where
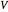 is velocity (m/s),
is velocity (m/s),
 is the density of the fluid (
is the density of the fluid (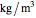 ),
),
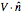 represents the product of the component of velocity normal to the control surface,
represents the product of the component of velocity normal to the control surface,
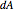 is the differential area of the control surface (
is the differential area of the control surface (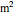 ).
).
Application of the momentum equation to the contents of the control volume yields:
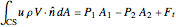 ,
,
where
 is velocity (m/s),
is velocity (m/s),
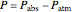 is gage pressure (kPa),
is gage pressure (kPa),
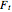 is the thrust force (N).
is the thrust force (N).
For one-dimensional flow:
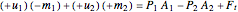 .
.
Due to conservation of mass 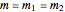 :
:
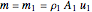 ,
,
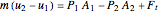 ,
,
using the ideal gas law:
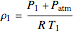 ,
,
where
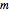 is the mass flow rate (kg/s)
is the mass flow rate (kg/s)
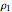 is the density of air at the inlet (
is the density of air at the inlet (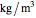 ),
),
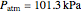 is atmospheric pressure,
is atmospheric pressure,
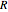 is the ideal gas constant,
is the ideal gas constant,
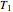 is temperature (K).
is temperature (K).
The continuity equation is used to determine the velocity of air exiting the turbine:
 ,
,
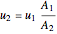 ,
,
where 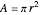 and
and  is the radius (m).
is the radius (m).
Solving for the thrust force:
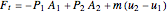 .
.
Reference
[1] B. R. Munson, T. H. Okiishi and W. W. Huebsch, Fundamentals of Fluid Mechanics, 6th ed., Hoboken, NJ: John Wiley & Sons, 2009.
Permanent Citation