Minimally Squared Rectangles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
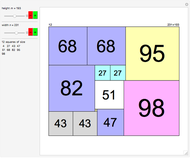
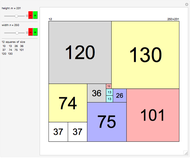
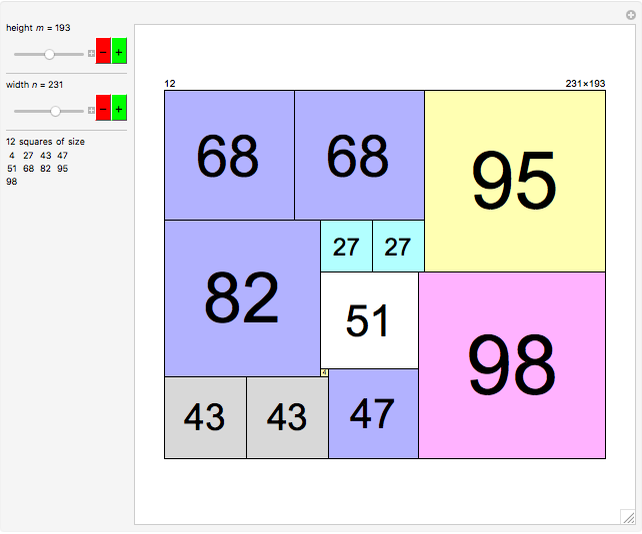
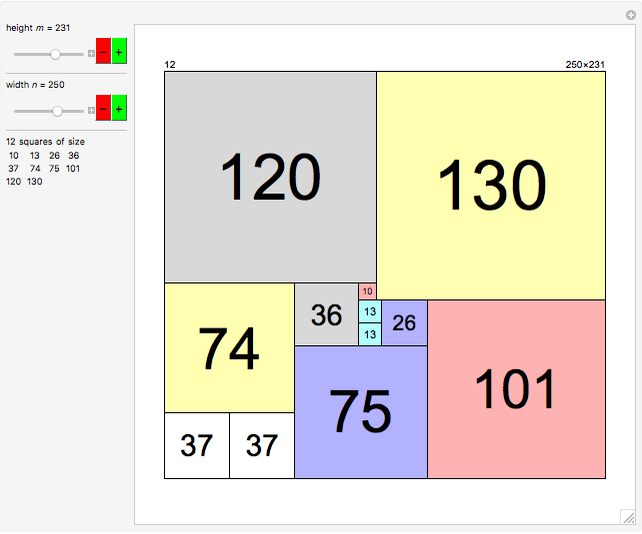
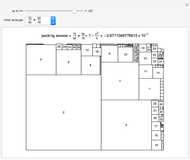
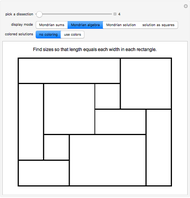
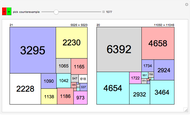
Divide a rectangle of size 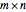 into the minimal number of squares. For a rectangle of size 17×19, the solution (with nine squares) is nontrivial to find. This Demonstration gives precalculated solutions for rectangles up to size 388×388.
into the minimal number of squares. For a rectangle of size 17×19, the solution (with nine squares) is nontrivial to find. This Demonstration gives precalculated solutions for rectangles up to size 388×388.
Contributed by: Ed Pegg Jr (March 2013)
Based on data compiled by Bertram Felgenhauer and Ed Pegg Jr
Open content licensed under CC BY-NC-SA
Details
Let 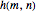 represent the minimal number of squares for an
represent the minimal number of squares for an 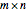 rectangle. Conjecture:
rectangle. Conjecture: 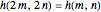 for all
for all 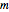 and
and  .
.
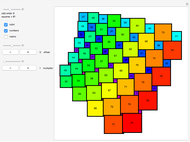
These solutions were compiled in the mistaken belief that a counterexample would be found. So far, the conjecture holds true for  . Solutions are found with a method involving Young tableaux; a single solution can require hours to find [1].
. Solutions are found with a method involving Young tableaux; a single solution can require hours to find [1].
Some rectangles can be divided into squares of different sizes. These are known as perfect rectangles, and are much easier to find [2].
References
[1] B. Felgenhauer. "Filling Rectangles with Integer-Sided Squares." (Mar 17, 2013) int-e.eu/~bf3/squares.
[2] S. Anderson. "Squaring.Net 2013." (Mar 26, 2013) www.squaring.net.
Snapshots
Permanent Citation