Mohr's Circle and Failure Criterion for Planar Stress States

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
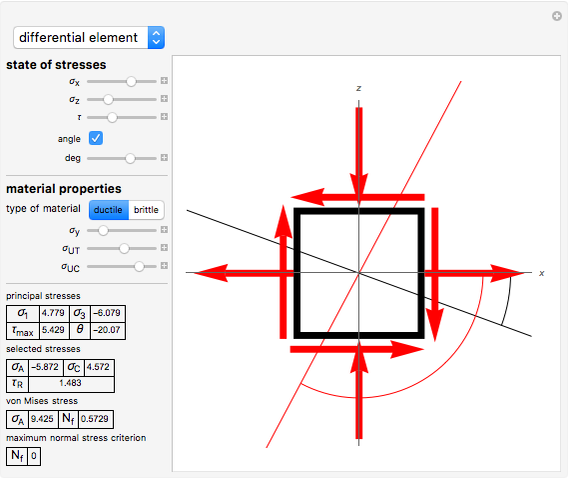
This Demonstration calculates the principal stresses and direction angle for a differential element and shows the following:
[more]
Contributed by: Felipe R. Amador V. (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
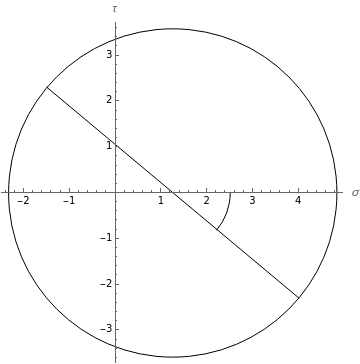
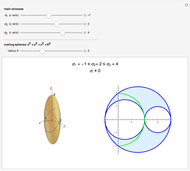
For the design of machinery, it is important to calculate the state of stresses for some critical points of a machine part. The stresses at the point are represented by a differential element. To calculate the principal stresses 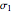 and
and 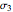
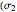 is not included as this is a planar stress), we use Mohr's circle, which is a graphical method to calculate the stresses of the element for a specified angle. Then the principal stresses occur at the intersection of the circle and the
is not included as this is a planar stress), we use Mohr's circle, which is a graphical method to calculate the stresses of the element for a specified angle. Then the principal stresses occur at the intersection of the circle and the  axis.
axis.
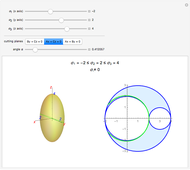
Finally, to determine if an element fails for a specified material, we enter three material properties: the yield strength 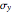 and the ultimate strength for tension and compression
and the ultimate strength for tension and compression 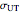 and
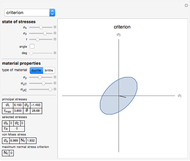
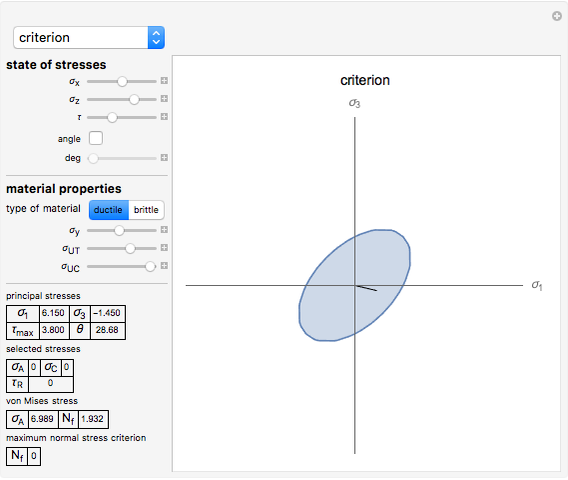
and 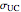 , respectively. Then if the material is ductile, the safety factor appears on the von Mises stress section. (The safety factor
, respectively. Then if the material is ductile, the safety factor appears on the von Mises stress section. (The safety factor 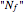 is the relation between the failure stress and the real stress that an element is subjected to;
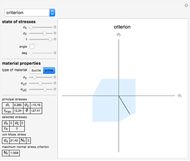
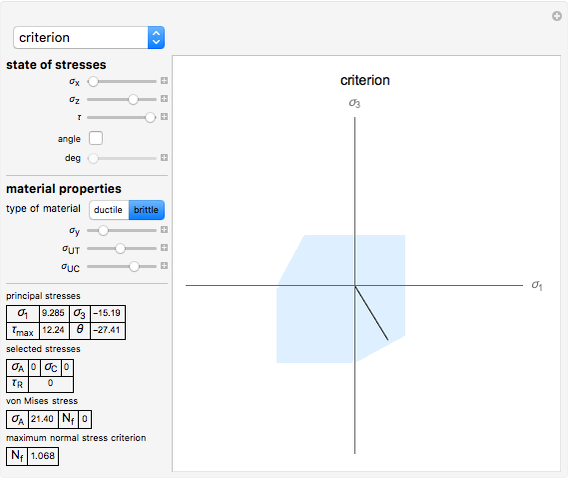
is the relation between the failure stress and the real stress that an element is subjected to; 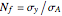 for a ductile material, for example.) A graphical representation of the safe zone is also shown; if the principal stresses fall within the safe zone, the element does not fail. For brittle materials, the safety factor appears in the maximum normal stress criterion section and its corresponding graphical representation also appears for the safe zone of a brittle material.
for a ductile material, for example.) A graphical representation of the safe zone is also shown; if the principal stresses fall within the safe zone, the element does not fail. For brittle materials, the safety factor appears in the maximum normal stress criterion section and its corresponding graphical representation also appears for the safe zone of a brittle material.
To use this program:
• Vary the state of the plane stresses for the differential element (compression values with negative sign and shearing stresses as shown in the text).
• Check the "angle" box for selected angles  . This angle rotates clockwise with respect to the
. This angle rotates clockwise with respect to the  axis and is colored red.
axis and is colored red.
• Enter the material properties of a selected material and look up the results.
• The results can be viewed using the popup menu at the top (the criterion depends on the type of material, whether brittle or ductile).
The conventions are the same as that used in [1].
Reference
[1] F. P. Beer, E. R. Johnston, Jr., J. T. DeWolf, and D. F. Mazurek, Mechanics of Materials, 6th ed., New York: McGraw–Hill, 2011.
Permanent Citation