Rotating Cubes about Axes of Symmetry; 3D Rotation Is Non-Abelian

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
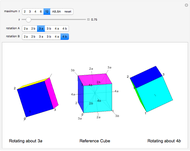
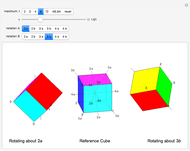
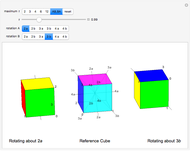
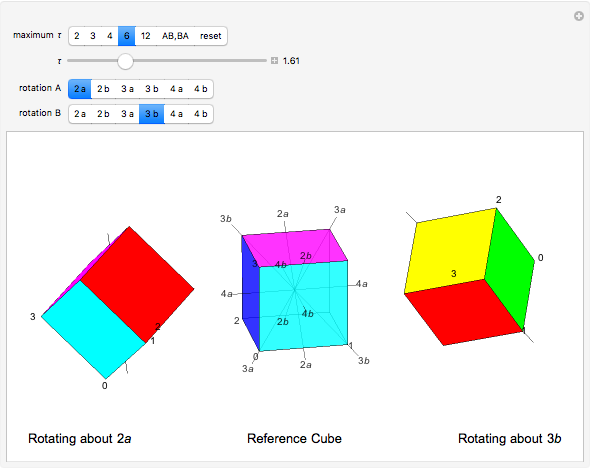
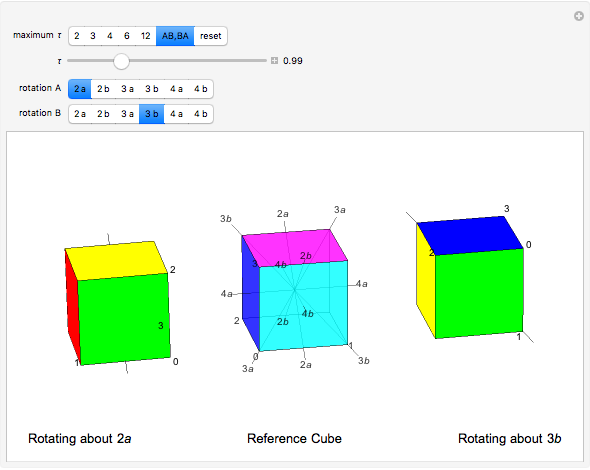
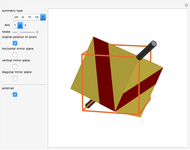
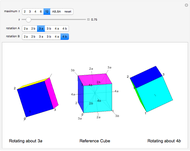
A cube has rotational axes of symmetry through the centers of a pair of opposite edges (two-fold symmetry, six axes), two opposite corners (three-fold symmetry, four axes), or the centers of two opposite faces (four-fold symmetry, three axes). The middle cube shows two examples of each axis; it is slightly transparent. Markers 0, 1, 2, and 3 are always visible, marking the vertices  ,
, 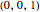 ,
, 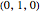 , and
, and 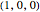 of each cube. Move the
of each cube. Move the  slider. The left cube rotates about the
slider. The left cube rotates about the 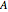 axis and the right rotates about the
axis and the right rotates about the 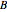 axis; the axes appear as stubs on the cubes. When
axis; the axes appear as stubs on the cubes. When  is an integer, the edges are once more parallel to the central cube, demonstrating the symmetry, but the original coloring is not recovered until
is an integer, the edges are once more parallel to the central cube, demonstrating the symmetry, but the original coloring is not recovered until  equals the axis number. Try different pairs of axes and change
equals the axis number. Try different pairs of axes and change  . You can click the picture and drag to alter the viewpoint.
. You can click the picture and drag to alter the viewpoint.
Contributed by: Roger Beresford (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
An uncolored cube has rotational symmetry; this is Abelian and is not demonstrated here.
In elementary mathematics the order of operations does not matter, that is, 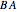 gives the same result as
gives the same result as 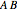 . This simplifying assumption leads to many "common-sense" notions that have to be unlearned on proceeding to "higher" mathematics.
. This simplifying assumption leads to many "common-sense" notions that have to be unlearned on proceeding to "higher" mathematics.
Permanent Citation