The Cake Icing Puzzle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
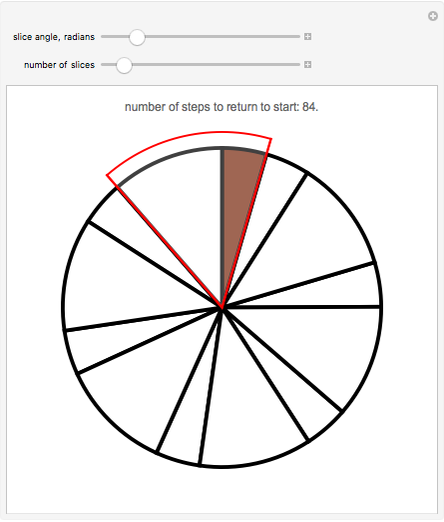
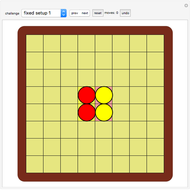
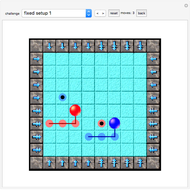
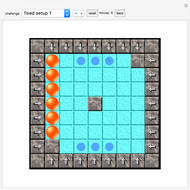
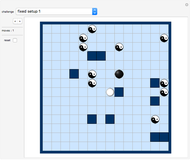
Take a cake with icing on the top and no icing on the bottom. Pick an angle  , cut a piece out of the cake in the usual way with center angle
, cut a piece out of the cake in the usual way with center angle  , turn the piece upside down, and replace it in the gap in the cake. Then do it again, with a piece that borders the initial piece. Keep doing this, moving in the same direction, thus forming cut lines at
, turn the piece upside down, and replace it in the gap in the cake. Then do it again, with a piece that borders the initial piece. Keep doing this, moving in the same direction, thus forming cut lines at  ,
,  ,
, 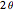 ,
, 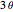 , and so on.
1. Will it ever happen, after the first inverting operation, that the cake is in its initial position, with all of the icing on the top?
2. Will it ever happen that all the icing is on the bottom?
Of course, if
, and so on.
1. Will it ever happen, after the first inverting operation, that the cake is in its initial position, with all of the icing on the top?
2. Will it ever happen that all the icing is on the bottom?
Of course, if  is a right angle, for example, then the answers are clearly YES and YES after eight and four cuts, respectively. But what if
is a right angle, for example, then the answers are clearly YES and YES after eight and four cuts, respectively. But what if  is not a rational multiple of
is not a rational multiple of  , say
, say  radian?
radian?
Contributed by: Stan Wagon (Macalester College) (March 2011)
Open content licensed under CC BY-NC-SA
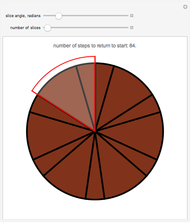
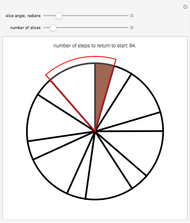
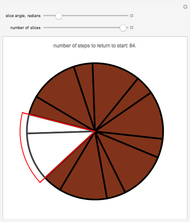
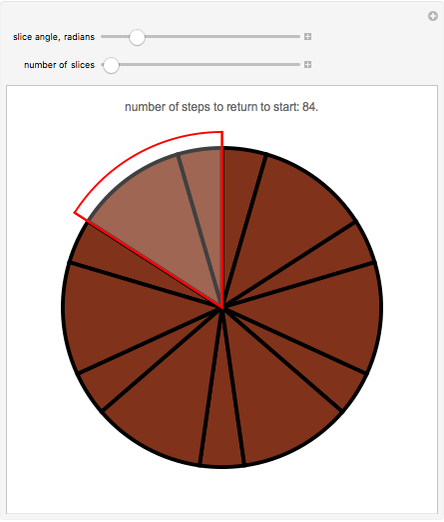
Snapshots
Details
This puzzle first appeared in the 31st Moscow Mathematical Olympiad. The complete solution can be found in the book by P. Winkler, Mathematical Mind-Benders, Natick, MA: AK Peters, 2007. If  is the smallest integer greater than or equal to
is the smallest integer greater than or equal to 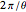 , then the icing covers the top of the cake after
, then the icing covers the top of the cake after 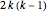 iterations (unless
iterations (unless 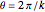 , in which case it takes
, in which case it takes 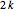 iterations). The icing will never all be on the bottom of the cake (unless
iterations). The icing will never all be on the bottom of the cake (unless 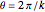 , in which case this happens after
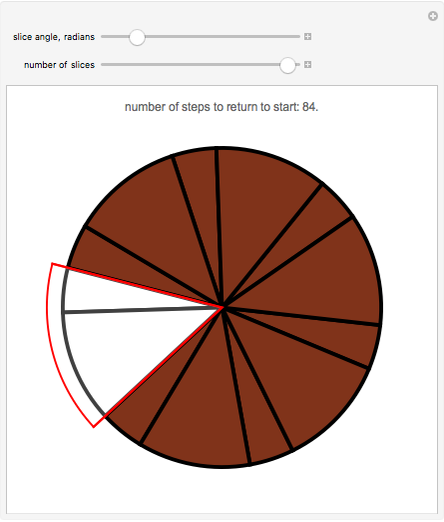
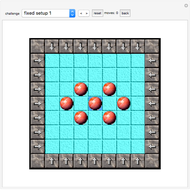
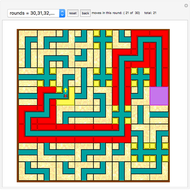
, in which case this happens after  iterations). Snapshot 3 shows the situation after 83 cuts for the case
iterations). Snapshot 3 shows the situation after 83 cuts for the case  ,
,  , and
, and 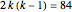 ; one more operation restores all the icing.
; one more operation restores all the icing.
Permanent Citation