Transfer Function for Continuous-Mode Boost Converter

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
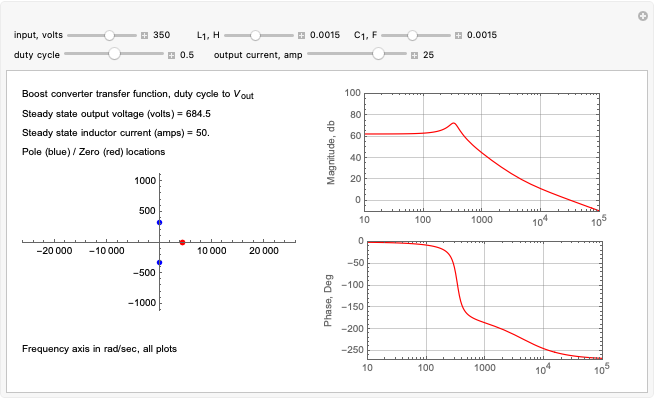
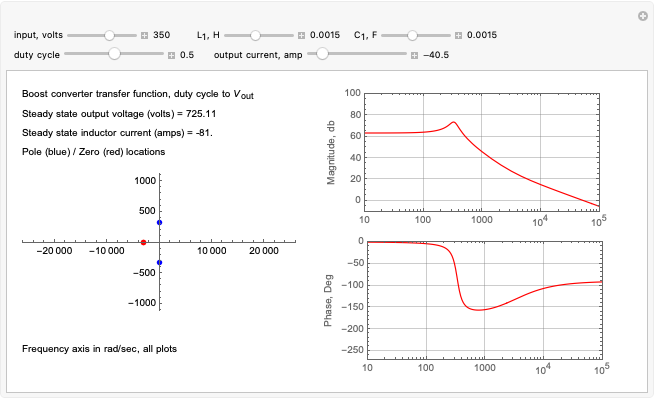
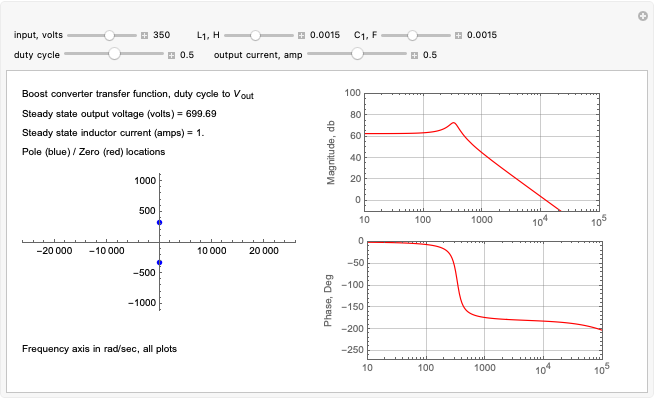
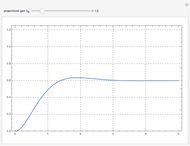
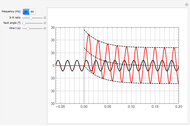
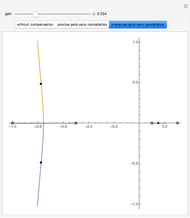
This Demonstration models the averaged transfer function of a continuous-mode boost power converter. The pole and zero locations are plotted on the complex plane, and the gain and phase are shown in the frequency domain. Note how the zero location changes as you vary the inductor current direction and magnitude.
[more]
Contributed by: Gary Baker (January 2012)
Open content licensed under CC BY-NC-SA
Details
The continuous-mode boost converter transfer function from duty cycle to output voltage contains a real zero along with a complex pole pair. The location of the zero changes with inductor current and is located in the right half of the complex plane when the power transfer is from input to output (this implementation has bidirectional current flow). The right half-plane zero (RHP zero) increases the gain and increases phase shift at the same time, making control stability challenging.
Snapshots
Permanent Citation