Tries

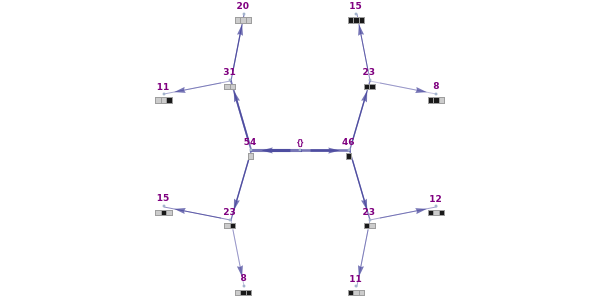
A "trie" is a data structure that converts "sentences" of symbols into a tree structure. In a trie all sequences ("n-grams") up to a certain length that appear in a "sentence" have as their parent "most" of that -gram, that is, all but the rightmost element of the original -gram. One also generally stores information on the number of times that a given -gram appears as the child of other -grams. Tries are useful for many purposes, including searching and finding "collocations", that is, -grams that appear more frequently than would occur randomly given their constituent parts.

In this Demonstration you create "sentences" by selecting an elementary cellular automaton rule and then choosing some rows of its evolution. Each row represents a sentence (although unlike linguistic sentences, the rows are "periodic", in the sense that the right end is connected with the left end). You also select the maximum size of the -grams you wish to appear in the trie. The system responds with a visualization of the trie as a network in which the nodes are the -grams (labeled in purple with the number of times they are hit by an incoming edge) and the thickness of the edges likewise reflects the number of times one particular -gram follows another.