Convolution Sum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
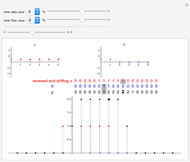
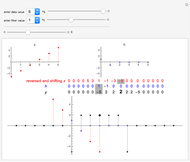
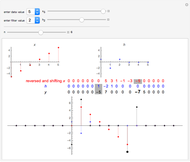
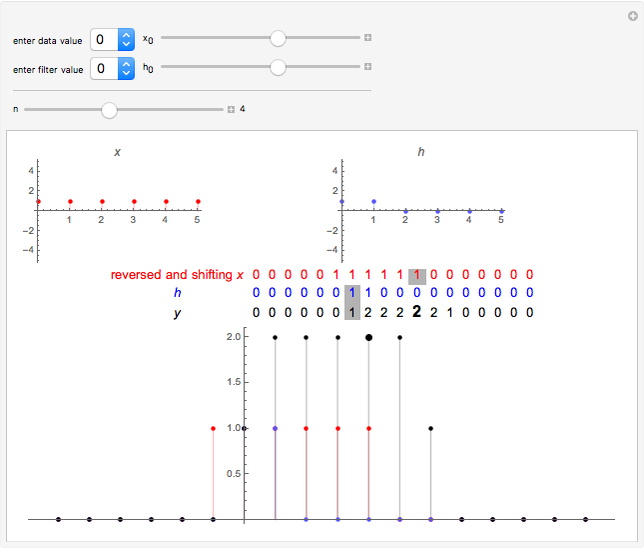
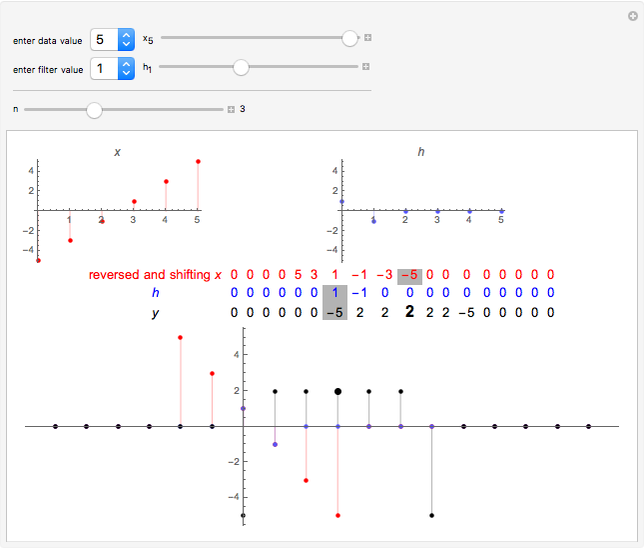
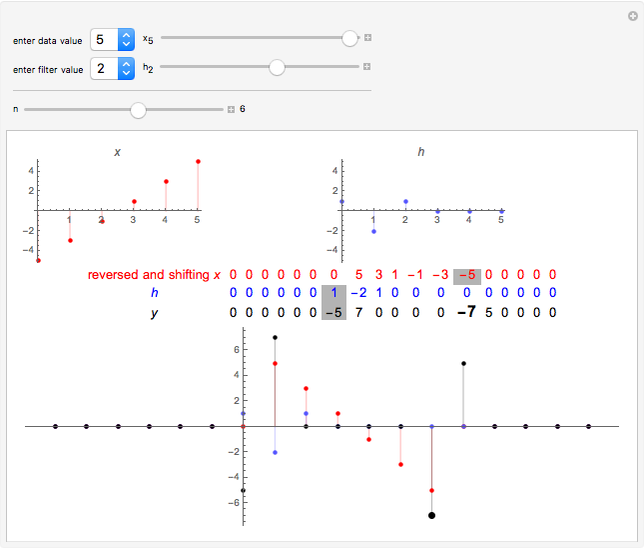
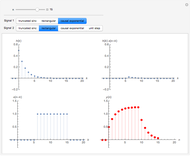
The  component of the convolution of
component of the convolution of  and
and  is defined by
is defined by 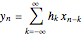 . Note that
. Note that 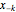 is the sequence
is the sequence 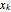 written in reverse order, and
written in reverse order, and 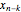 shifts this sequence
shifts this sequence  units right for positive
units right for positive  . Thus one can think of the component
. Thus one can think of the component 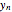 as an inner product of
as an inner product of  and a shifted reversed
and a shifted reversed  . For purposes of illustration
. For purposes of illustration  and
and  can have at most six nonzero terms corresponding to
can have at most six nonzero terms corresponding to 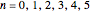 . These terms are entered with the controls above the delimiter. In the table the gray-shaded cells mark the position
. These terms are entered with the controls above the delimiter. In the table the gray-shaded cells mark the position  . The bold number in the table and larger point on the plot indicate
. The bold number in the table and larger point on the plot indicate 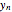 .
.
Contributed by: Bruce Atwood (Beloit College) (June 2009)
Suggested by: Patrick Van Fleet (University of St. Thomas)
Open content licensed under CC BY-NC-SA
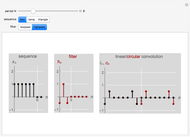
Snapshots
Details
Convolution is a topic that appears in many areas of mathematics: algebra (finding the coefficients of the product of two polynomials), probability, Fourier analysis, differential equations, number theory, and so on. One important application is processing a signal by a filter. For more information see P. J. Van Fleet, Discrete Wavelet Transformations, Hoboken, New Jersey: John Wiley & Sons, Inc., 2008.
In signal processing the list  is the data or input signal and the kernel
is the data or input signal and the kernel  is a filter or the response to a unit impulse for a linear time-invariant system. There are several examples in the bookmarks to look at and explore by modifying the terms of
is a filter or the response to a unit impulse for a linear time-invariant system. There are several examples in the bookmarks to look at and explore by modifying the terms of  and
and  . Students might want to think about and then experiment with this Demonstration to answer the following questions: (1) what
. Students might want to think about and then experiment with this Demonstration to answer the following questions: (1) what  scales
scales  by a constant? (2) what
by a constant? (2) what  would cause
would cause 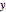 to be a delayed version of
to be a delayed version of  ? and (3) what interpretation would you give to convolving a signal with itself?
? and (3) what interpretation would you give to convolving a signal with itself?
Except for padded zeros at the beginning and end of 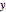 , this Demonstration replicates the output of the Mathematica command ListConvolve[h, x, {1, -1}, 0]. Additional interesting applications can be found in the Mathematica help for ListConvolve, at this link.
, this Demonstration replicates the output of the Mathematica command ListConvolve[h, x, {1, -1}, 0]. Additional interesting applications can be found in the Mathematica help for ListConvolve, at this link.
Permanent Citation