Wolfram Demonstrations Project

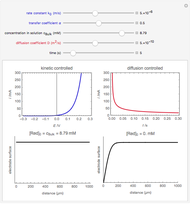
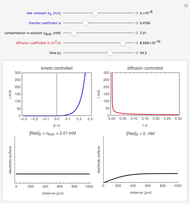
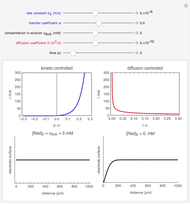
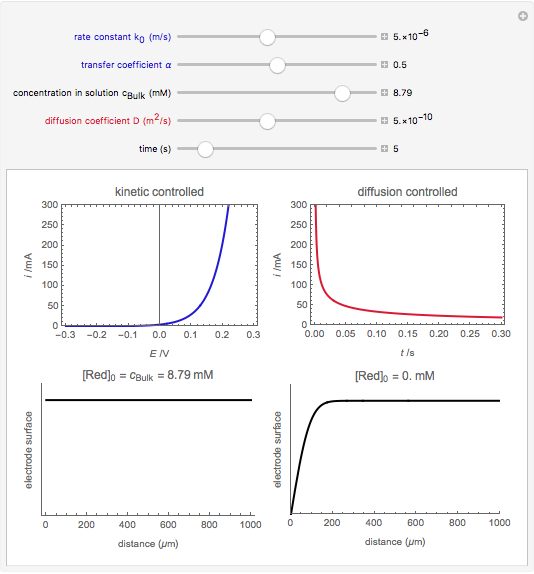
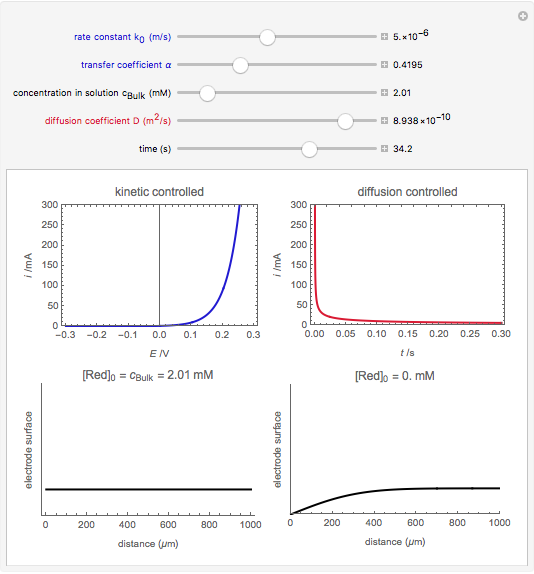
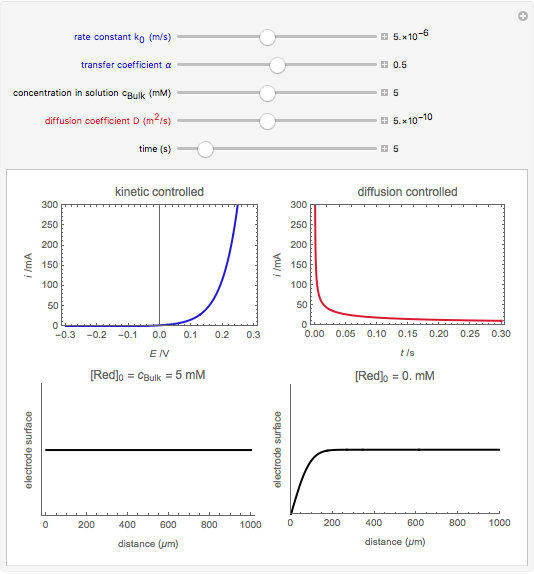
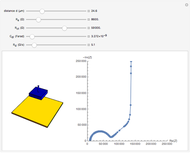
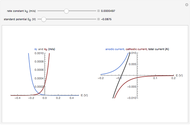
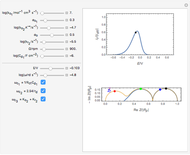
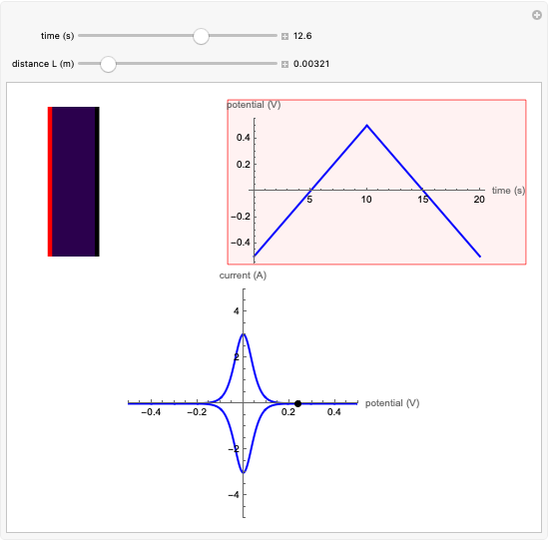
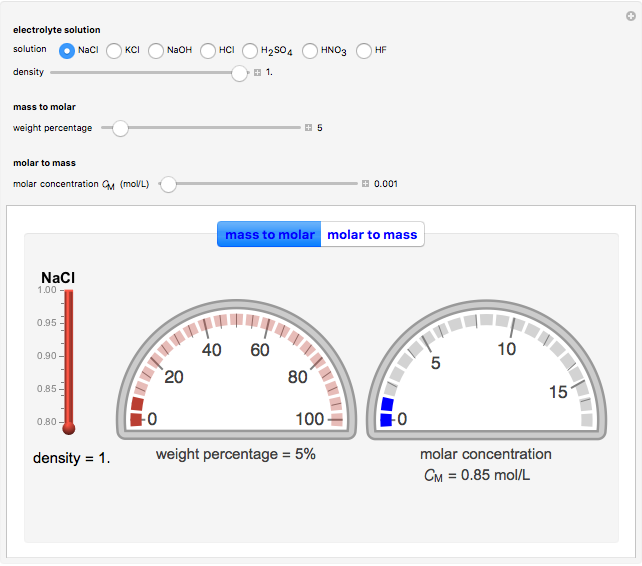
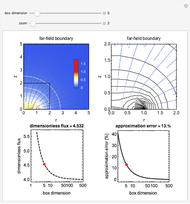
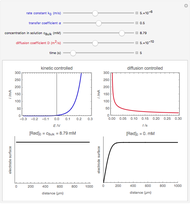
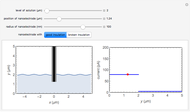
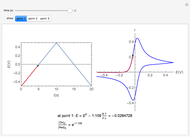
An electrochemical reaction on the surface of an electrode can occur by two limiting mechanisms: the reaction is controlled by kinetics and the reaction is controlled by the diffusion of the electroactive species. When the diffusion of the species is infinitely fast, the phenomenon is controlled by kinetics. When the kinetics are extremely fast, the phenomenon is controlled by the diffusion (mass transport) of the species that enters or leaves the electrode surface. This Demonstration shows the current on the left (blue) when controlled by kinetics and on the right (red) when controlled by diffusion.

Contributed by: Quang-Dao Trinh

Slider Zoom
Automatic Animation

At the electrode surface, the redox reaction can be written: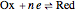

. Assume that there is only reductor in the solution with concentration

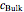(mM).

When the diffusion is very fast, the current depends only on the kinetics. Because of the fast diffusion, the concentration at the surface of the electrode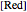

is equal to the concentration in the bulk solution:

The reaction rates of the oxidation direction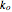

depend on the applied potential

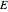at the electrode:

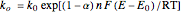, (1)

where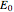

(in V) is the standard potential of the redox reaction,

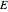is the applied potential,

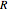is the gas constant (8.314 J/K mol),

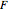is the Faraday constant (96485 C/mol),

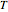(in K) is the temperature,

is the number of electrons transferred,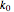

is the standard heterogeneous rate constant (in m/s), and

is the transfer coefficient.

Then current is calculated from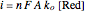

, where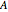

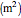is the surface area of the electrode, and

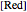is the concentration of the reductor at the surface of the electrode.

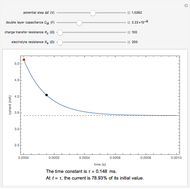
When the kinetics are very fast, the concentration at the surface of electrode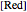

is always zero (

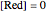) because the reductor is oxidized very quickly. Then the current depends on the diffusion of the reductor from the bulk solution to the electrode surface. The current in this case depends on the rate of diffusion at the surface

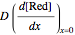, given by

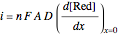, (2)

where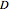

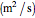is the diffusion coefficient.

This Demonstration shows that when the diffusion occurs (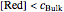

) one must use equation (2) instead of equation (1) to calculate the current. The kinetics-controlled case is simpler than the diffusion-controlled case because the diffusion equation (a partial differential equation) must be solved. In this Demonstration, equation (3), a Cottrell equation, is used for a large electrode with planar diffusion.