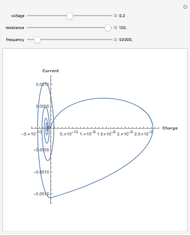
RLC Tank Circuit Bandpass Filter: Triangle Waveform Input

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Contributed by: Michael R. Braunstein (February 2012)
(Central Washington University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The solution of this system proceeds from an inhomogeneous linear differential equation governing the circuit, applying Kirchoff’s voltage law, Kirchoff’s current law, and the idealized electronic behavior of resistors (Ohm’s law), capacitors, and inductors.
1. When the inhomogeneity is sinusoidal with angular frequency  , the particular (steady-state) solution of the differential equation is sinusoidal with the same frequency, and the problem reduces to solving for the amplitude and phase of the solution. The ratio of the amplitude to the input amplitude for a particular frequency is called the "gain" of the circuit for that frequency. Because of the (idealized) linear properties of resistors, capacitors, and inductors, all of the electronic dynamic properties of the circuit (voltages, currents, charges) are then also sinusoidal with only their amplitude and phase to be determined.
, the particular (steady-state) solution of the differential equation is sinusoidal with the same frequency, and the problem reduces to solving for the amplitude and phase of the solution. The ratio of the amplitude to the input amplitude for a particular frequency is called the "gain" of the circuit for that frequency. Because of the (idealized) linear properties of resistors, capacitors, and inductors, all of the electronic dynamic properties of the circuit (voltages, currents, charges) are then also sinusoidal with only their amplitude and phase to be determined.
2. Because the differential equation is linear, if the inhomogeneity is a superposition of sinusoidal functions of different frequencies, its particular (steady-state) solution is simply the superposition of the particular solutions for each frequency component.
3. The Fourier series formalism provides a means to represent any periodic function as a superposition of sinusoidal functions whose frequencies are integral multiples of its fundamental frequency (harmonics). Combined with 1 and 2, this formalism then provides a general algorithm for describing the response of a linear electronic circuit to a periodic input signal.
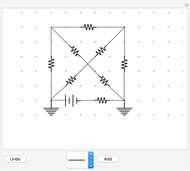
The component values for the circuit represented in this Demonstration are: 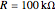 ,
, 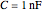 ,
, 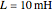 ,
, 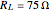 , and
, and 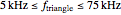 , all of which correspond to components that are readily available, and a circuit using these can be investigated in detail with an inexpensive oscilloscope and function generator. The components yield a resonant frequency for the circuit of approximately 50 kHz.
, all of which correspond to components that are readily available, and a circuit using these can be investigated in detail with an inexpensive oscilloscope and function generator. The components yield a resonant frequency for the circuit of approximately 50 kHz.
This Demonstration expresses the periodic triangle waveform input as a Fourier series (for a triangle waveform only the odd harmonics are nonzero, and their amplitude in the series falls off rapidly for higher-frequency harmonics) and then performs the superposition of the appropriate gain-attenuated and phase-shifted harmonic components to obtain the output of the circuit. Ten terms of the Fourier series provide sufficient resolution for the purposes of this Demonstration.
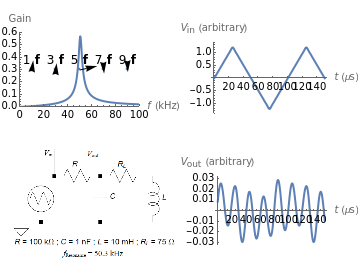
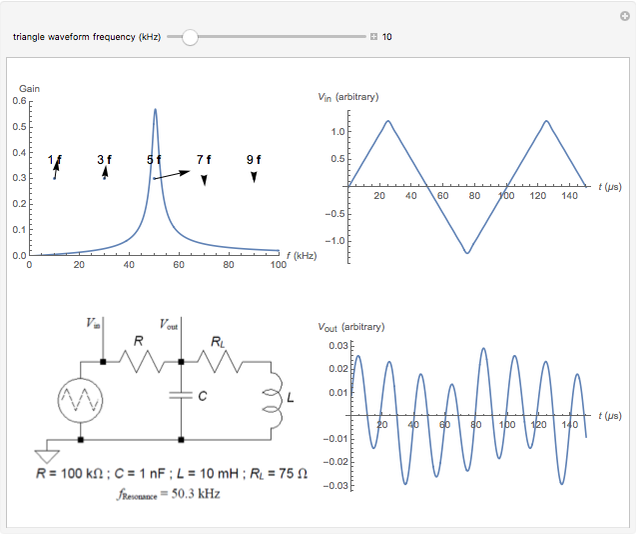
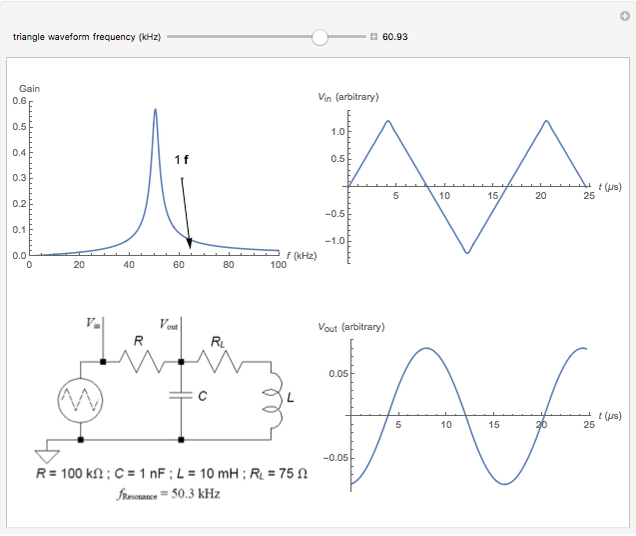
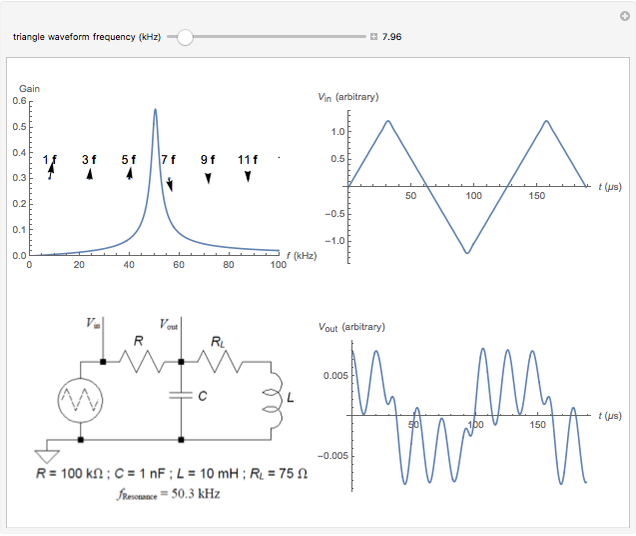
The right side of the result lets you examine the output of the circuit for inputs that are triangle waveforms with a range of frequencies, and is structured similarly to the displayed response of the circuit on an oscilloscope: the horizontal axis is time and the vertical axis is amplitude with the upper graph (trace) corresponding to the input and the lower graph (trace) to the output.
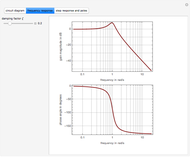
The left side of the result shows the gain curve of the 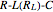 tank circuit bandpass filter with the gain for a sinusoidal waveform input frequency on the vertical axis and its frequency on the horizontal axis. It demonstrates that sinusoidal waveforms with frequencies either well below or well above the resonant frequency are significantly attenuated while sinusoidal waveforms with frequencies close to the resonant frequency are relatively less attenuated. (A more quantifiable version of the expressions "well below", "well above", and "close to" would involve a parameter of the system known as its
tank circuit bandpass filter with the gain for a sinusoidal waveform input frequency on the vertical axis and its frequency on the horizontal axis. It demonstrates that sinusoidal waveforms with frequencies either well below or well above the resonant frequency are significantly attenuated while sinusoidal waveforms with frequencies close to the resonant frequency are relatively less attenuated. (A more quantifiable version of the expressions "well below", "well above", and "close to" would involve a parameter of the system known as its 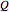 value, beyond the scope of this Demonstration.)
value, beyond the scope of this Demonstration.)
In addition, the gain curve plot shows phasors representing the odd harmonics of the fundamental frequency of the triangle waveform frequency that has been selected. Each phasor is labeled as its multiple of the fundamental frequency and its origin is located horizontally at its frequency (the vertical position of its origin in the plot is arbitrary). The length of each phasor represents the square-root-scaled relative amplitude of that harmonic component in the output (the relative amplitude is the product of the filter gain for that frequency with its coefficient in the Fourier series for the input waveform). The angle of each phasor with respect to the horizontal shows the phase for that harmonic component in the output relative to the harmonic component in the input waveform. For a phasor that points horizontally to the right its phase difference between the output and input harmonic components is zero, for a phasor that points vertically up the output harmonic component leads the input harmonic component by 90 degrees, for one that points vertically down the output harmonic component lags the input harmonic component by 90 degrees, and so on.
Finally, the lower-left corner of the panel shows a schematic diagram of the circuit.
Some significant things to notice:
• When one of the harmonics is close to the resonant frequency it dominates the structure of the output.
• When one of the higher harmonics of the fundamental frequency is close to the resonant frequency the output waveform looks somewhat like the harmonic modulated by the fundamental.
• When a harmonic is at the resonant frequency its phase is 0.
• When a harmonic is lower in frequency than the resonant frequency it leads the harmonic component of the input.
• When a harmonic is higher in frequency than the resonant frequency it lags the harmonic component of the input.
Permanent Citation