Three-Branch Electrical Circuit

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
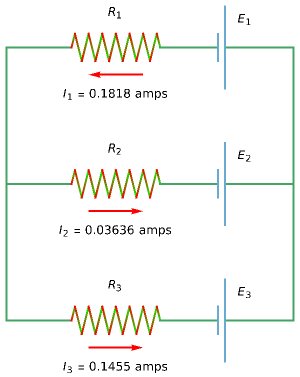
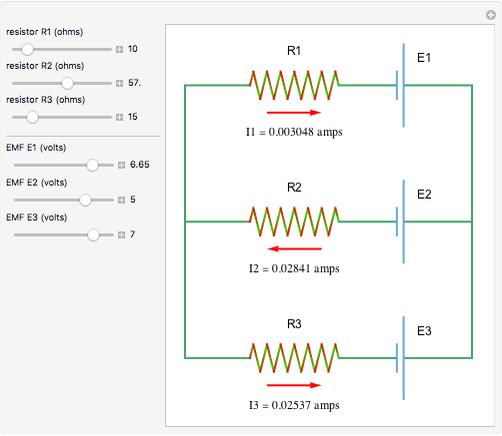
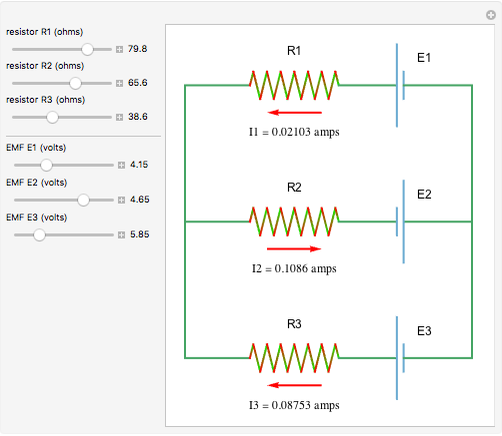
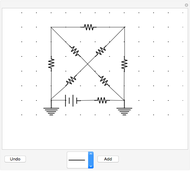
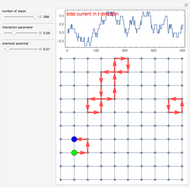
This Demonstration shows a current distribution for a simple three-branch electrical circuit. This is a classic textbook example that cannot be reduced to independent parallel and series connections and therefore requires the use of Kirchhoff's rules.
Contributed by: Darya Aleinikava (August 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration helps to visualize the current distribution in a simple three-branch electric circuit. The problem corresponds to the Physics II curriculum of the majority of technical colleges in the United States. It can be used as a teaching aid during classroom presentations or homework assignments.
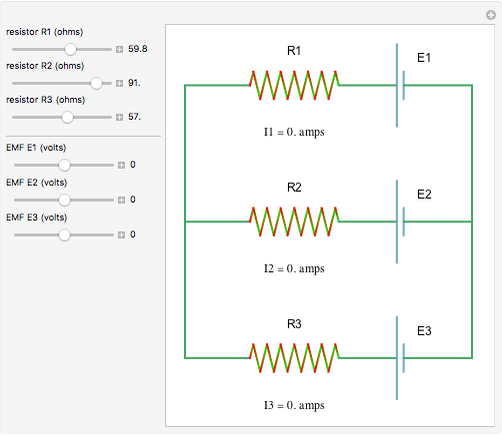
The controls for EMFs and resistances show the "power play" between different batteries striving to push currents in their "preferred" directions. When all batteries are equivalent, none of them "wins" and the currents are 0 in all branches.
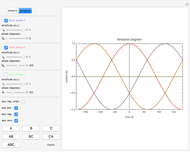
The currents 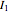 ,
, 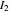 , and
, and 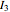 are found as the solutions of a system of algebraic equations derived from Kirchhoff's rules. The arrows denote the directions of conventional currents.
are found as the solutions of a system of algebraic equations derived from Kirchhoff's rules. The arrows denote the directions of conventional currents.
Kirchhoff's first rule: At any junction point in a circuit, the sum of the currents into the junction must equal the sum of the currents out of the junction. Kirchhoff's second rule: When any closed circuit loop is traversed, the algebraic sum of the potential differences must add to zero.
Permanent Citation