The Gravitational Two-Body Problem in the Einstein-Infeld-Hoffmann Approximation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration displays the orbits of the two-body problem in general relativity in various ways. Several simplifications are involved: separating off the trivial center of mass motion, restricting to bounded motion in a plane, and neglecting the emission of gravitational radiation. Actually, we use a Hamiltonian formulation of the work by Einstein [1] on gravitating particles. The Hamilton function is the sum of the nonrelativistic term that defines the Kepler problem and a relativistic term of order 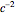 that takes into account velocity-dependent masses and retardation. The function is simple enough that Hamilton's canonical equations of motion can be solved by Mathematica's built-in function NDSolve for given initial conditions and a given number of revolutions (say four) within fractions of a second.
that takes into account velocity-dependent masses and retardation. The function is simple enough that Hamilton's canonical equations of motion can be solved by Mathematica's built-in function NDSolve for given initial conditions and a given number of revolutions (say four) within fractions of a second.
Contributed by: Ulrich Mutze (July 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
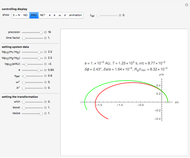
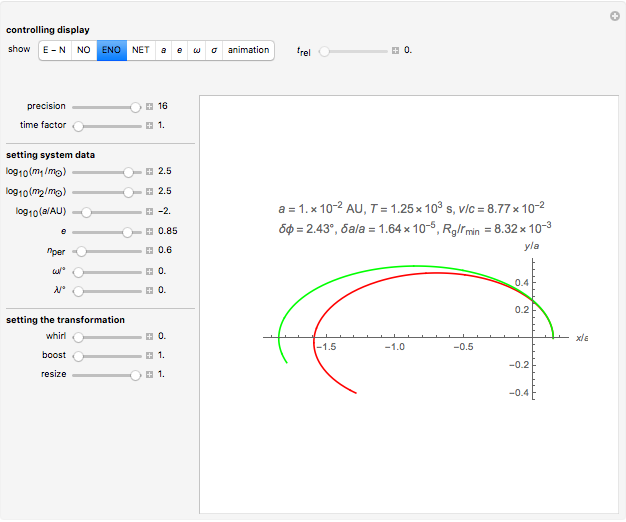
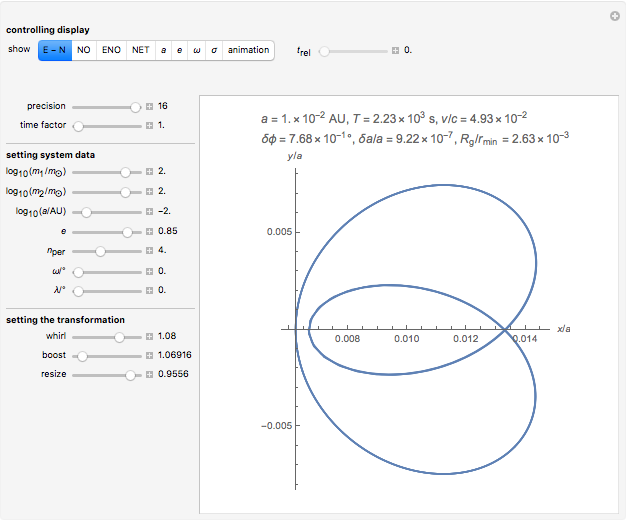
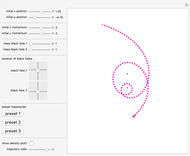
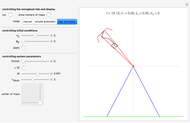
Snapshot 1: osculating trajectories: an Einstein trajectory (red) and a Newton/Kepler trajectory with the same initial state
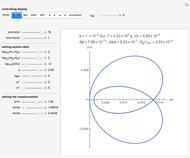
Snapshot 2: residual motion
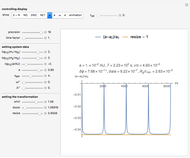
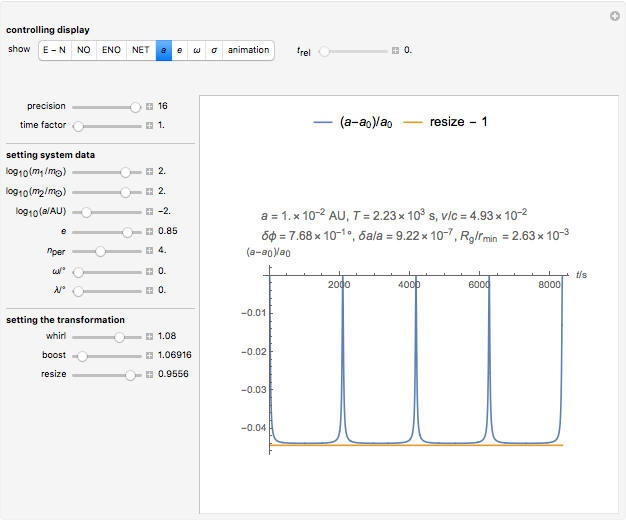
Snapshot 3: periodic half-axis variation along an Einstein trajectory; vary "resize"
Snapshot 4: evolution of the longitude of perihelion (periastron, ...) along an Einstein trajectory; vary "whirl".
Snapshot 5: evolution of the reduced mean longitude along an Einstein trajectory; vary "boost"
Snapshot 6: combined rotation and scaling transforms bring the Einstein trajectory and the Newton trajectory to coincide well
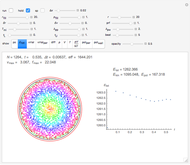
Two dynamical systems are under consideration. They are labeled N (for Newton) and E (for Einstein), occupying the same phase space with dynamical variables 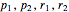 and parameters
and parameters 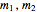 . Their dynamics are defined by the Hamilton functions:
. Their dynamics are defined by the Hamilton functions: 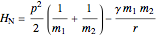 ,
, 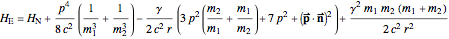 , where
, where 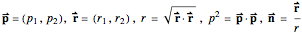 (taken verbatim from [2]). The N-system is well-known from the Kepler problem. Its trajectories can be characterized by four orbital elements, here denoted by
(taken verbatim from [2]). The N-system is well-known from the Kepler problem. Its trajectories can be characterized by four orbital elements, here denoted by  ,
,  ,
,  ,
,  . The display NO shows the Kepler orbit for the orbital elements set by the corresponding sliders.
. The display NO shows the Kepler orbit for the orbital elements set by the corresponding sliders.
The idea of this Demonstration is to study the effects brought about by replacing 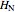 by
by 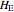 , in the spirit of perturbation theory. As all textbooks on general relativity explain, an elliptic orbit becomes a rosette-shaped non-closed orbit (see thumbnail). This solves an intensively-discussed puzzle of nineteenth-century astronomy: that the perihelion of the planet Mercury moves a bit faster than could be explained in terms of gravitational forces from known, or even from hypothetical, planets. As a once very popular astronomy book [3] puts it (my translation): "Under these circumstances the opinion broke ground that Newton's law of gravity would not hold to absolute precision".
, in the spirit of perturbation theory. As all textbooks on general relativity explain, an elliptic orbit becomes a rosette-shaped non-closed orbit (see thumbnail). This solves an intensively-discussed puzzle of nineteenth-century astronomy: that the perihelion of the planet Mercury moves a bit faster than could be explained in terms of gravitational forces from known, or even from hypothetical, planets. As a once very popular astronomy book [3] puts it (my translation): "Under these circumstances the opinion broke ground that Newton's law of gravity would not hold to absolute precision".
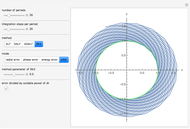
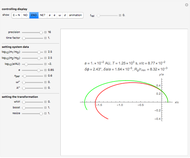
This Demonstration lets you consider systems of stars or Schwarzschild black holes for which the effect of the non-Newtonian part of the Hamiltonian function is much larger than in the case of Mercury. It originated from the question of how accurately an E-trajectory can be described as a rotating N-trajectory. The method of investigation is to apply to the E-trajectory a suitable counter-rotation 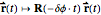 with the
with the 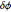 slider selected as a free multiple of the value given by the standard formula for the Mercury perihelion problem. In this way we can make a closed stationary orbit, and the question is how the associated trajectory is related to some osculating N-trajectory. It turns out that the osculating N-trajectory to the initial state comes close if space coordinates are multiplied by a certain factor less than 1 and time is multiplied by a certain factor greater than 1. These factors can be set by sliders and one appears to be able to always bring the trajectories close together.
slider selected as a free multiple of the value given by the standard formula for the Mercury perihelion problem. In this way we can make a closed stationary orbit, and the question is how the associated trajectory is related to some osculating N-trajectory. It turns out that the osculating N-trajectory to the initial state comes close if space coordinates are multiplied by a certain factor less than 1 and time is multiplied by a certain factor greater than 1. These factors can be set by sliders and one appears to be able to always bring the trajectories close together.
The remaining difference trajectory, here referred to as residual motion, shows interesting properties. It can often be made virtually periodical for many revolutions, drawing a residual orbit that changes from a circle-like loop to a pretzel loop (see snapshot 2) when the system becomes "more relativistic". This experimental transformation method is supplemented by a conventional one, where the orbital elements of osculating Kepler orbits are represented graphically as functions of time in a way that suitable parameters for the transformation method can be set under visual control (see snapshots 3, 4, 5).
References
[1] A. Einstein, L. Infeld, and B. Hoffmann, "The Gravitational Equations and the Problem of Motion," Annals of Mathematics, 2nd series, 39(1), 1938 pp. 65–100. www.jstor.org/stable/1968714.
[2] L. D. Landau and E. M. Lifschitz, Lehrbuch der Theoretschen Physik, Volume II, Berlin: Akademie-Verlag, 1984 p. 409 (1).
[3] J. Littrow, Die Wunder Des Himmels, (revised by Edmund Weiß), Berlin: Verlag Ferdinand Dümmler, 1897 p. 308.
Permanent Citation