Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Time Series for Power-Law Decay

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

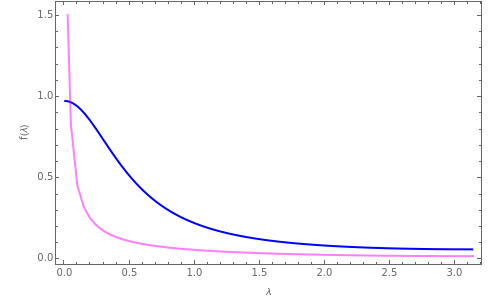
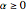Power-law decay time series are characterized by autocorrelation functions that decay as , where is the lag and is the decay parameter. When 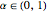, the time series exhibits strong persistence, with smaller values of indicating stronger persistence. When 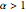, the time series exhibits high-frequency (or alternating) behavior and is said to be anti-persistent. Such time series are also characterized by a spectral density function that is proportional to 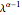, where 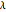is the radial frequency.

[more]

This Demonstration investigates four basic types of power-law decay time series—HD (hyperbolic decay model), FD (fractionally differenced white noise), FGN (fractional Gaussian noise), and PPL (pure power-law process)—by simulating a series of length and displaying one of five selected graphs: the time series plot (data), the autocorrelation function (ACF), the partial autocorrelation (PACF), the periodogram, and the spectral density function (SDF). In each case, blue represents the data or sample estimate and magenta represents the expected value.

[less]

Contributed by: Justin Veenstra and Ian McLeod (November 2012)
(Western University)
Open content licensed under CC BY-NC-SA

Snapshots

Details

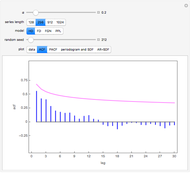
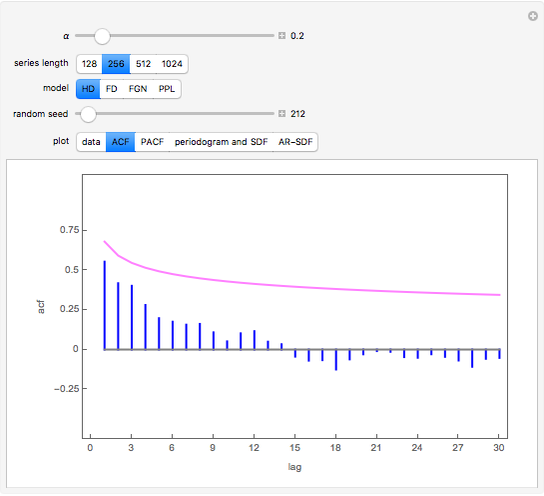
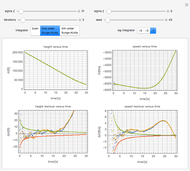
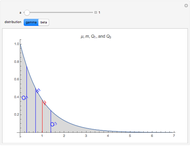
Snapshot 1: This shows the autocorrelation for FGN with 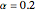and series length 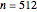. The setting 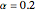corresponds to a Hurst coefficient of 0.9, which indicates very strong persistence. We see there is a large bias in the usual sample autocorrelation, since the true value is always much larger, except at lag 1.

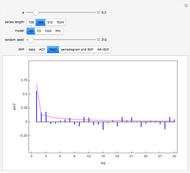
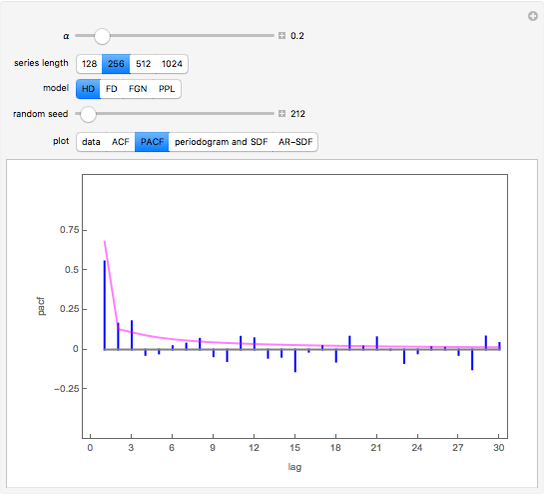
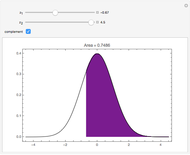
Snapshot 2: This shows the partial autocorrelation for the same data used in snapshot 1. The partial autocorrelation was estimated using the Burg algorithm, and it seems to do a better job.

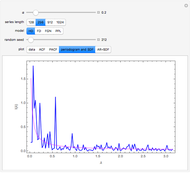
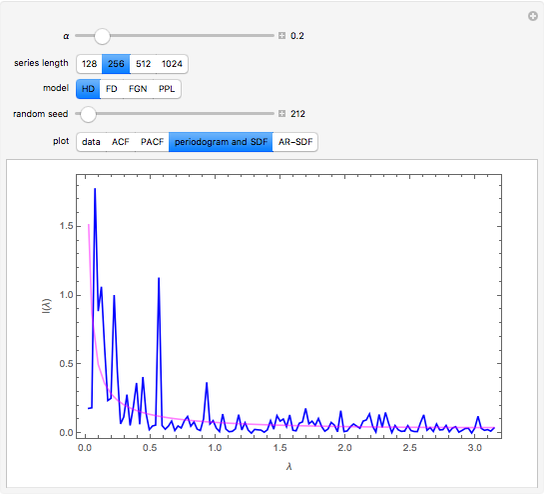
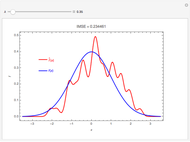
Snapshot 3: The periodogram and its expected value, the SDF, are shown.

Snapshot 4: The SDF is shown in magenta along with its estimate in blue. The SDF is estimated by fitting an AR model using the Burg algorithm with model order determined using the AIC criterion.

For an overview and further references for the time series models, see [1].

Reference

[1] J. Q. Veenstra and A. I. McLeod, "A New Hyperbolic Decay Time Series Model," 2012. Submitted for publication.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send