Electromagnetic Wave from Dipole over a Perfect Conductor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
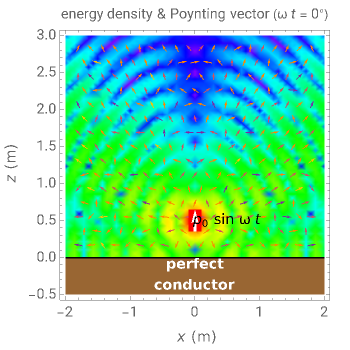
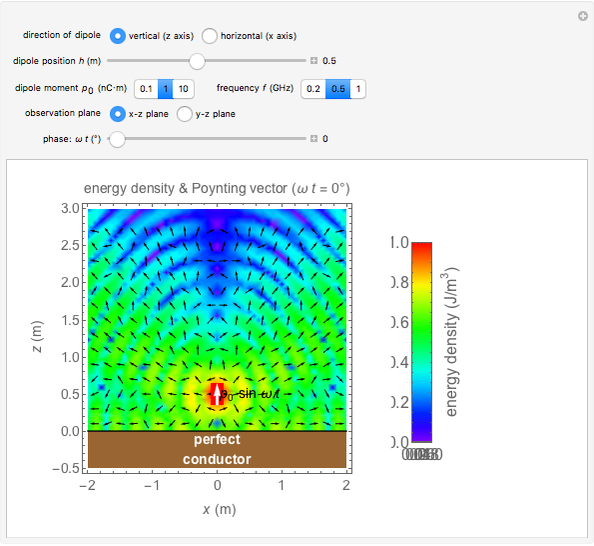
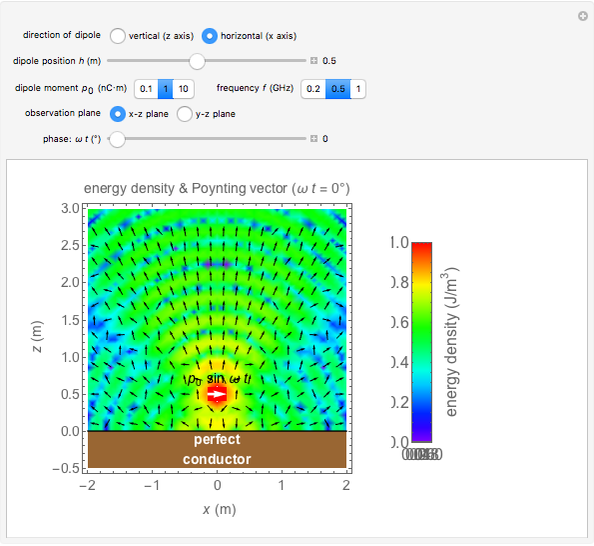
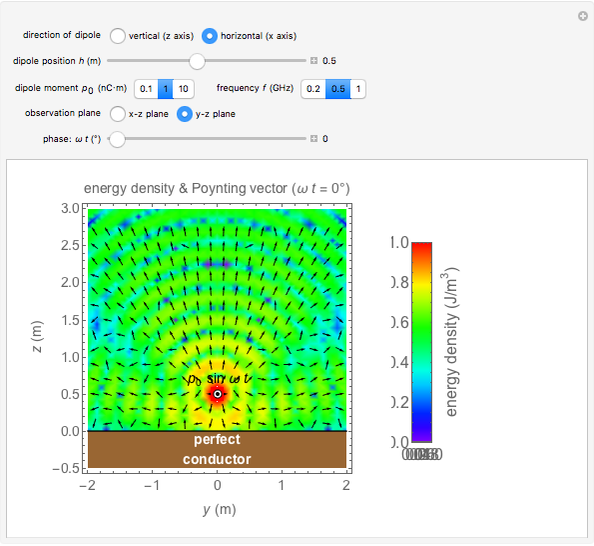
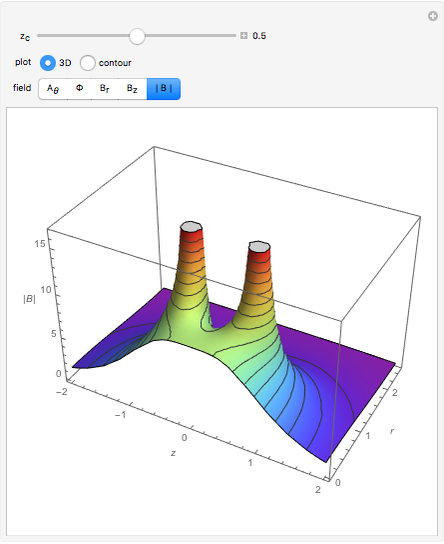
This Demonstration shows the electromagnetic field for an electric dipole placed over a perfect conductor. The spatial distributions of energy density and the Poynting vector are shown for varying dipole direction, observation plane, and time. You can also vary the distance between dipole and the plane  , the amplitude of the dipole moment
, the amplitude of the dipole moment 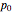 , and the frequency
, and the frequency 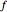 . The energy density pattern is shown in color on a logarithmic scale, and the Poynting vector is mapped by arrows.
. The energy density pattern is shown in color on a logarithmic scale, and the Poynting vector is mapped by arrows.
Contributed by: Y. Shibuya (November 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
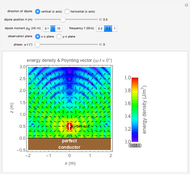
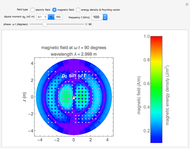
Snapshot 1: vertically oriented dipole
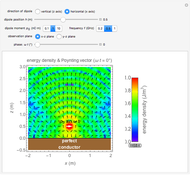
Snapshot 2: horizontally oriented dipole seen from the side
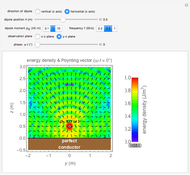
Snapshot 3: horizontally oriented dipole seen head-on
The electromagnetic fields of a dipole located over the perfect conductor can be analyzed assuming an image inside the conductor. For example, in the vertical case, the (electrical) Hertz vector can be expressed as
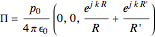 ,
,
where 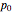 is the dipole amplitude,
is the dipole amplitude, 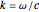 is the wave number, and
is the wave number, and 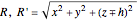 are the distances between the dipole and observation points. Then, the electric and magnetic fields can be calculated as follows:
are the distances between the dipole and observation points. Then, the electric and magnetic fields can be calculated as follows:
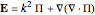 ,
, 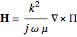 .
.
Then, energy density 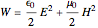 and the Poynting vector
and the Poynting vector 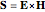 can be calculated, taking into account the time factors
can be calculated, taking into account the time factors  .
.
Either in the  -
- or
or 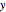 -
- planes, the Poynting vectors remain in the same plane, shown by arrows. The vertical case gives the same result for the
planes, the Poynting vectors remain in the same plane, shown by arrows. The vertical case gives the same result for the  -
- or
or 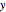 -
- planes; however, the horizontal case gives different results as seen in Snapshots 2 and 3.
planes; however, the horizontal case gives different results as seen in Snapshots 2 and 3.
Regarding the vertical and horizontal antennas as vertical and horizontal dipoles, the electromagnetic wave patterns of this Demonstration might be of use in understanding the efficiencies of vertical and horizontal antennas.
Reference
[1] A. Sommerfeld, Partial Differential Equations in Physics, (E.G. Strauss, trans.), New York: Academic Press, 1949.
Permanent Citation