Wolfram Demonstrations Project

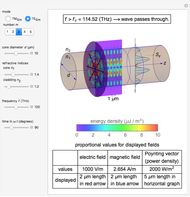
Light or other electromagnetic waves can propagate through optical fibers. This Demonstration visualizes the field, energy distribution, and propagation of light in step index fibers. A step index fiber is composed of a core and cladding that have different refractive indices

and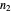

, respectively. Many modes are possible, including the transverse magnetic (TM) and transverse electric (TE) waves, of which the zeroth modes

and

are chosen here.

In this Demonstration, the instantaneous fields, energy density, and power density are displayed for the designated time

for a given mode number

, core diameter

, and the frequency

. The maximum electric field is fixed at 1000 V/m for all conditions. The frequency has to be higher than the cut-off frequency

determined by

and

. Using cylindrical coordinates with the wave propagation direction as the

axis, the fields are a function of

, and

. Energy flows along the channel (along the positive

direction). The electric and magnetic fields are shown on a perpendicular plane by red and blue arrows, respectively. The energy density is displayed on two planes by coloring. The energy transport or power density

(

component) is shown. The fields proportional to the magnitudes are displayed, with their relations listed in the table.

Contributed by: Y. Shibuya

Rotate and Zoom in 3D
Slider Zoom
Gamepad Controls
Automatic Animation

Snapshot 1: fields for

mode for a fiber of 10

m diameter at

Snapshot 2: fields of

mode for a fiber of 10

m diameter at

Snapshot 3: fields of

mode for a fiber of 10

m diameter at

The periodic solution of the wave equation for the modes

and

has to be axisymmetrical. In the case of

, for example, it takes the form

Here

is the core radius and

is the angular frequency. Considering the connection conditions for other field components leads to transcendental equations:

The values of

and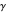

are the

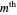roots of the characteristic equations. There is a cut-off frequency

determined by the fiber property and the value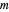

. The frequency has to be higher than

in order for there to be a solution for

and

. The cut-off frequency is the same for the TM and TE modes, but the values of

and

are different because of a slight difference in the characteristic equations. Once

and

are determined,

is obtained from the relation

. The constant

is set so that the maximum electric field is 1000 V/m. Other field components can then be readily calculated.

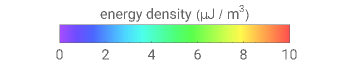
For the sake of simplicity, the electrical and magnetic fields are shown in the areas where the power flow is at a maximum. The energy density is calculated by