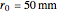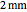Leakage Inductance in a Transformer

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Good electromagnetic coupling between the primary and secondary windings is normally achieved when the core has a high permeability. However, some leakage inductance is always present, related to transformer characteristics such as short circuit performance.
[more]
Contributed by: Y. Shibuya (September 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
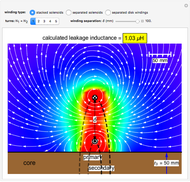
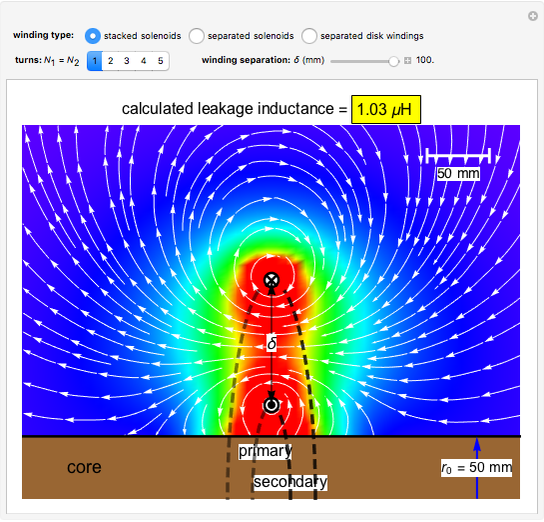
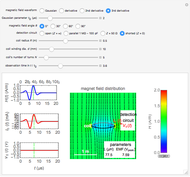
Snapshot 1: one-turn concentric windings separated by 100 mm
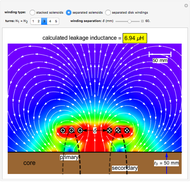
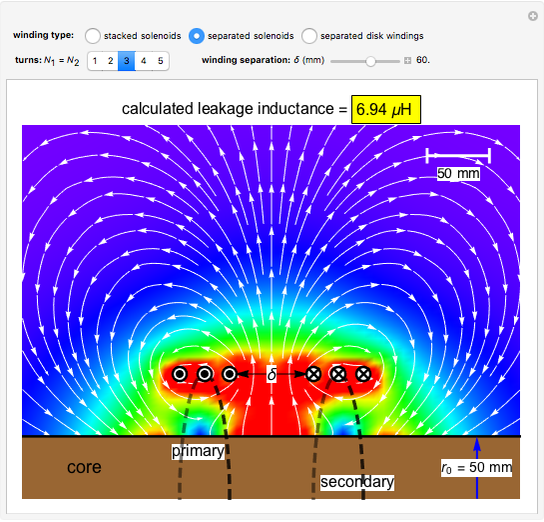
Snapshot 2: two solenoids separated by 60 mm
Snapshot 3: two disk windings separated by 80 mm
In the approximation we use, the winding ring current is accompanied by another ring current (i.e., image current) inside the core, due to its infinitely large core permeability. This approximation is by no means perfect, since the magnetic field does not intersect the core surface at right angles everywhere. Because the discrepancy occurs on the periphery, it may have a limited effect on the calculated leakage inductance.
By definition, the leakage inductance is proportional to the magnetic flux between two windings and the square of the number of turns. Calculations with a different number of turns and separation distances verify these relations.
Reference
[1] F. de Leon and A. Semlyen, "Efficient Calculation of Elementary Parameters of Transformers," IEEE Transactions on Power Delivery, 7(1), 1992 pp. 376–383. doi:10.1109/61.108931.
Permanent Citation
"Leakage Inductance in a Transformer"
http://demonstrations.wolfram.com/LeakageInductanceInATransformer/
Wolfram Demonstrations Project
Published: September 21 2016