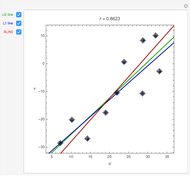
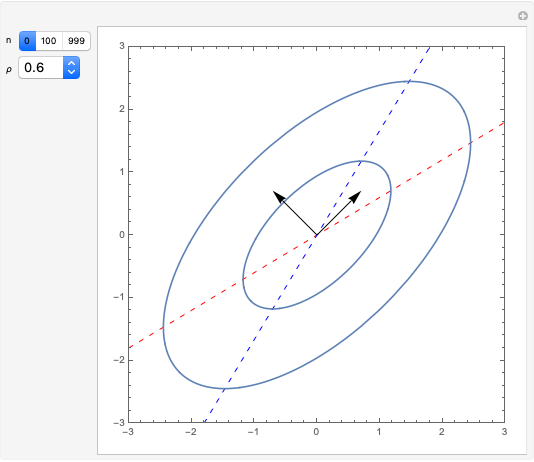
Influential Points in Regression

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
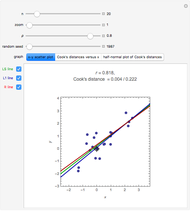
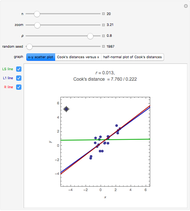
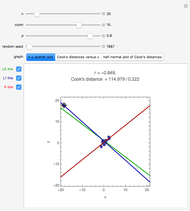
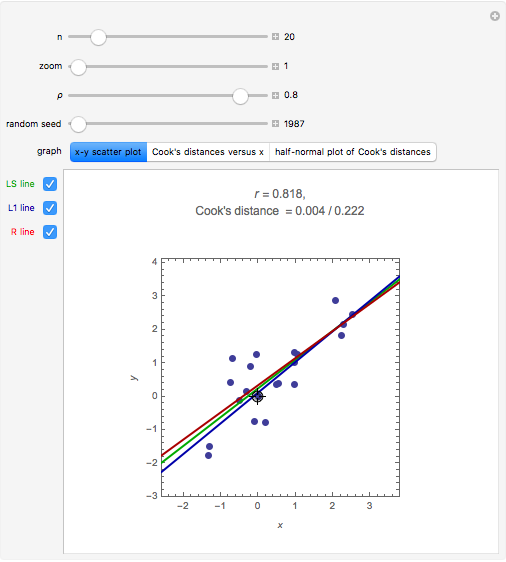
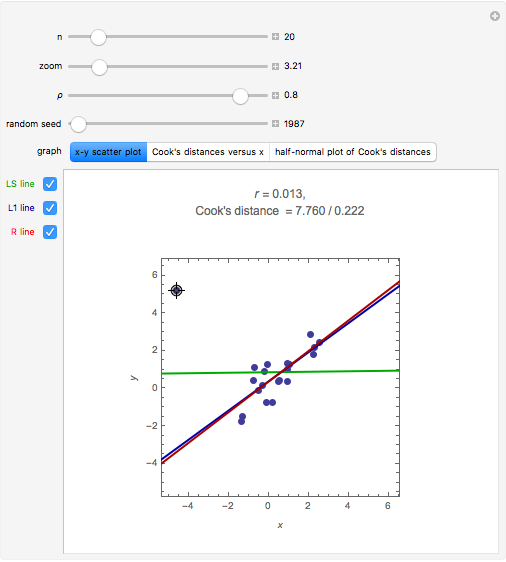
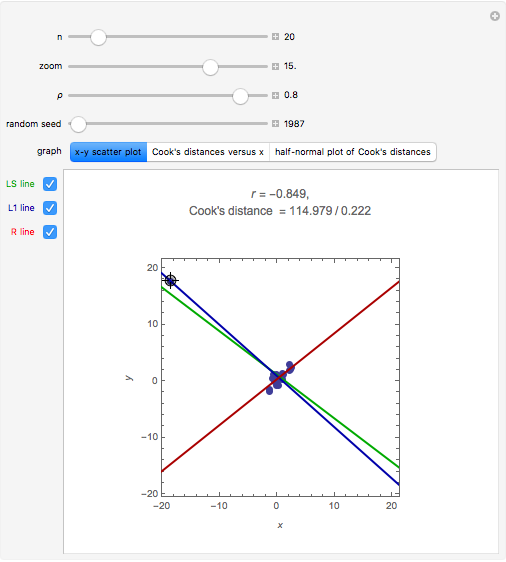
A random sample of size  from a bivariate normal distribution with mean
from a bivariate normal distribution with mean 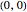 , unit variances, and correlation coefficient
, unit variances, and correlation coefficient  is generated. The sample correlation
is generated. The sample correlation  is shown as well as the Cook's distance corresponding to the locator point. Several methods of fitting the regression line are available.
is shown as well as the Cook's distance corresponding to the locator point. Several methods of fitting the regression line are available.
Contributed by: Ian McLeod (March 2011)
(University of Western Ontario)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For the definition of Cook's distance, see [1]. For discussion of its use in detecting influential points in regression, see [2, 3].
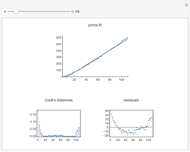
Pages 67–68 of [2] suggest that observations with Cook's distances with values exceeding 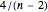 may be influential but that it is better to look at a plot of the Cook's distances versus
may be influential but that it is better to look at a plot of the Cook's distances versus  with a benchmark line at
with a benchmark line at  .
.
Page 70 of [3] suggests looking at the half-normal plot of the Cook's distances to see those that are relatively large compared with the rest.
L1 Regression: minimizes the absolute sum of errors. This is computed using linear programming; see eqn. (3) in [4]. L1 regression is more robust than LS when moderate outliers are present, but it is still sensitive to extreme outliers.
RLINE: resistant regression line, discussed in §5 of [5], is based on medians.
[1] Cook's distance, Wikipedia.
[2] S. J. Sheather, A Modern Approach to Regression with R, New York: Springer, 2009.
[3] J. J. Faraway, Linear Models with R, Boca Raton: Chapman & Hall/CRC, 2005.
[4] S. C. Narula and J. F. Wellington, "The Minimum Sum of Absolute Errors Regression: A State of the Art Survey," International Statistical Review, 50(2), 1982 pp. 317–326.
[5] P. F. Velleman and D. C. Hoaglin, Applications, Basics and Computing of Exploratory Data Analysis, Boston: Duxbury Press, 1981.
Permanent Citation